資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Javascript 實現 Prim 演算法
Prim 演算法是一種貪心演算法，用於查詢加權無向圖的最小生成樹。它找到邊的子集，形成包含每個頂點的樹，其中樹中所有邊的總權重最小。
該演算法透過一次一個頂點地構建這棵樹來執行，從一個任意的起始頂點開始，在每一步中新增從樹到另一個頂點的最便宜的連線。
Prim 演算法是如何工作的？
讓我們來看一下 Prim 演算法是如何工作的：
1. 選擇任意節點作為根節點：在本例中，我們選擇 S 節點作為 Prim 生成樹的根節點。這個節點是任意選擇的，因此任何節點都可以作為根節點。有人可能會問為什麼任何影片都可以是根節點。答案是，在生成樹中包含圖的所有節點，並且由於它是連通的，因此必須至少有一條邊將它連線到樹的其餘部分。
2. 檢查外向邊並選擇成本較低的邊：選擇根節點 S 後，我們看到 S，A 和 S，C 是兩條權重分別為 7 和 8 的邊。我們選擇邊 S，A，因為它小於另一條邊。
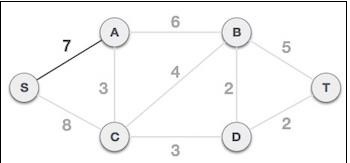
現在，樹 S-7-A 被視為一個節點，我們檢查所有從中出去的邊。我們選擇成本最低的邊並將其包含在樹中。
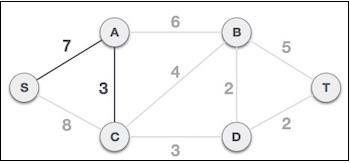
此步驟之後，形成 S-7-A-3-C 樹。現在我們將再次將其視為一個節點，並將再次檢查所有邊。但是，我們將只選擇成本最低的邊。在本例中，C-3-D 是新的邊，它小於其他邊的成本 8、6、4 等。
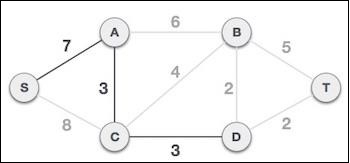
在將節點 **D** 新增到生成樹後，我們現在有兩條從中出去的邊具有相同的成本，即 D-2-T 和 D-2-B。因此，我們可以新增兩者中的任何一個。但是下一步將再次產生邊 2 作為最低成本。因此，我們正在顯示包含兩條邊的生成樹。
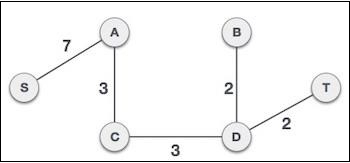
現在讓我們看看我們如何在程式碼中實現相同的演算法：
示例
primsMST() {
// Initialize graph that'll contain the MST
const MST = new Graph();
if (this.nodes.length === 0) {
return MST;
}
// Select first node as starting node
let s = this.nodes[0];
// Create a Priority Queue and explored set
let edgeQueue = new PriorityQueue(this.nodes.length * this.nodes.length);
let explored = new Set();
explored.add(s);
MST.addNode(s);
// Add all edges from this starting node to the PQ taking weights as priority
this.edges[s].forEach(edge => {
edgeQueue.enqueue([s, edge.node], edge.weight);
});
// Take the smallest edge and add that to the new graph
let currentMinEdge = edgeQueue.dequeue();
while (!edgeQueue.isEmpty()) {
// COntinue removing edges till we get an edge with an unexplored node
while (!edgeQueue.isEmpty() && explored.has(currentMinEdge.data[1])) {
currentMinEdge = edgeQueue.dequeue();
}
let nextNode = currentMinEdge.data[1];
// Check again as queue might get empty without giving back unexplored element
if (!explored.has(nextNode)) {
MST.addNode(nextNode);
MST.addEdge(currentMinEdge.data[0], nextNode, currentMinEdge.priority);
// Again add all edges to the PQ
this.edges[nextNode].forEach(edge => {
edgeQueue.enqueue([nextNode, edge.node], edge.weight);
});
// Mark this node as explored explored.add(nextNode);
s = nextNode;
}
}
return MST;
}您可以使用以下方法進行測試
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C", 100);
g.addEdge("A", "B", 3);
g.addEdge("A", "D", 4);
g.addEdge("C", "D", 3);
g.addEdge("D", "E", 8);
g.addEdge("E", "F", 10);
g.addEdge("B", "G", 9);
g.primsMST().display();輸出
這將給出以下輸出：
A->B, D B->A, G D->A, C, E C->D E->D, F G->B F->E
請注意，我們的初始圖是：
示例
/** * A * / | \ * C | B * \ | | * D G * | / * E * | * F */
輸出
我們當前的圖如下所示：
/** * A * |\ * C | B * \ | | * D G * | * E * | * F * */
我們已經去掉了成本最高的邊，現在得到了一棵生成樹。
更新於：2020年6月15日
2K+ 次瀏覽
廣告