資料結構
網路
關係資料庫管理系統（RDBMS）
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究懸式絕緣子串上的電位分佈
懸式絕緣子
懸式絕緣子由若干個瓷質圓盤透過金屬連線件串聯而成，形成一個串，如圖 1 所示。
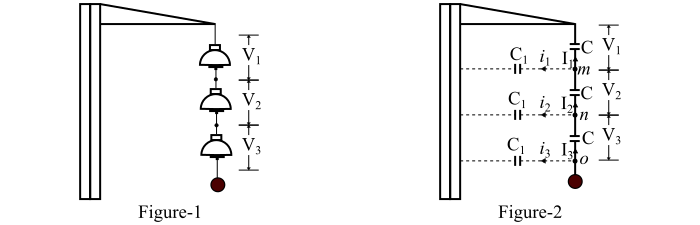
懸式絕緣子串上的電位分佈
我們知道，懸式絕緣子串由多個瓷質圓盤透過金屬連線件串聯而成。每個圓盤的瓷質部分位於兩個金屬連線件之間。因此，圓盤就像一個電容器，用 C 表示，如圖 2 所示。
電容 C 稱為**互電容**。如果串聯只有互電容，則所有圓盤的充電電流將相同，因此每個圓盤上的電壓也相同（例如 V/3），如圖 2 所示。但在實際應用中，每個圓盤的金屬配件與鐵塔之間也存在電容。這種電容稱為旁路電容，在圖 2 中用 C1 表示。
由於旁路電容的存在，所有圓盤的充電電流並不相同，即每個圓盤上的電壓也不相同。最靠近導線的圓盤電壓最高。
因此，關於懸式絕緣子串上電位分佈的重要觀察結果如下：
由於旁路電容的存在，懸式絕緣子串上的電壓不會均勻地分佈在各個圓盤上。
最靠近導線的圓盤電壓最高，隨著靠近橫擔，電壓逐漸降低。
如果施加在串上的電壓為直流電，則每個圓盤上的電壓將相同，因為絕緣子的電容對直流電不起作用。
懸式絕緣子串上電位分佈的數學分析
參考圖 2。設旁路電容C1是自感（C）的某個分數K，即，𝐶1=𝐾𝐶。從橫擔開始，每個圓盤上的電壓分別為V1、V2和V3。
將基爾霍夫電流定律應用於節點m，我們有：
$$\mathrm{\mathit{I_{\mathrm{2}}\mathrm{\, =\, }I_{\mathrm{1}}\mathrm{\, +\, }i_{\mathrm{1}}}}$$
$$\mathrm{\mathit{\Rightarrow \omega \, CV_{\mathrm{2}}\mathrm{\, =\, }\omega \, CV_{\mathrm{1}}\mathrm{\, +\, }\omega \, C_{\mathrm{1}}V_{\mathrm{1}}}}$$
$$\mathrm{\mathit{\Rightarrow \omega \, CV_{\mathrm{2}}\mathrm{\, =\, }\omega \, CV_{\mathrm{1}}\mathrm{\, +\, }\omega \, KCV_{\mathrm{1}}}}$$
$$\mathrm{\mathit{\Rightarrow V_{\mathrm{2}}\mathrm{\, =\, }V_{\mathrm{1}}\left ( \mathrm{1}\mathrm{\, +\, }K \right )}\: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$
將基爾霍夫電流定律應用於節點n，我們有：
$$\mathrm{\mathit{I_{\mathrm{3}}\mathrm{\, =\, }I_{\mathrm{2}}\mathrm{\, +\, }i_{\mathrm{2}}}}$$
$$\mathrm{\mathit{\Rightarrow \omega \, CV_{\mathrm{3}}\mathrm{\, =\, }\omega \, CV_{\mathrm{2}}\mathrm{\, +\, }\omega \, C_{\mathrm{1}}\left ( V_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{2}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow \omega \, CV_{\mathrm{3}}\mathrm{\, =\, }\omega \, CV_{\mathrm{2}}\mathrm{\, +\, }\omega \, KC\left ( V_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{2}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow V_{\mathrm{3}}\mathrm{\, =\, }V_{\mathrm{2}}\mathrm{\, +\, }\left ( V_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{2}} \right )K}} $$
$$\mathrm{\mathit{\Rightarrow V_{\mathrm{3}}\mathrm{\, =\, }KV_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{2}}\left ( \mathrm{1}\mathrm{\, +\, }K \right )}}$$
$$\mathrm{\mathit{\Rightarrow V_{\mathrm{3}}\mathrm{\, =\, }KV_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{1}}\left ( \mathrm{1}\mathrm{\, +\, }K \right )^{\mathrm{2}}\mathrm{\, =\, }V_{\mathrm{1}}\left [ K\mathrm{\, +\, }\left ( \mathrm{1}\mathrm{\, +\, }K \right )^{\mathrm{2}} \right ]}}$$
$$\mathrm{\mathit{\therefore V_{\mathrm{3}}\mathrm{\, =\, }V_{\mathrm{1}}\left [ \mathrm{1\mathrm{\, +\, }3}K\mathrm{\, +\, }K^{\mathrm{2}} \right ] }\: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$
現在，導體和橫擔之間的電壓為
$$\mathrm{\mathit{V\mathrm{\, =\, }V_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{2}}\mathrm{\, +\, }V_{\mathrm{3}}}}$$
$$\mathrm{\mathit{V\mathrm{\, =\, }V_{\mathrm{1}}\mathrm{\, +\, }V_{\mathrm{1}}\left ( \mathrm{1}\mathrm{\, +\, }K \right )\mathrm{\, +\, }V_{\mathrm{1}}\left [ \mathrm{1\mathrm{\, +\, }3}K\mathrm{\, +\, }K^{\mathrm{2}} \right ]}}$$
$$\mathrm{\mathit{\Rightarrow V\mathrm{\, =\, }V_{\mathrm{1}}\left (K^{\mathrm{2}}\mathrm{\, +\, } \mathrm{4}K \mathrm{\, +\, }\mathrm{3}\right )}}$$
$$\mathrm{\mathit{\therefore V\mathrm{\, =\, }V_{\mathrm{1}}\left (\mathrm{1}\mathrm{\, +\, }K\right )\left ( \mathrm{3}\mathrm{\, +\, }K \right )}\: \: \: \cdot \cdot \cdot \left ( 3 \right )} $$
根據公式 (1)、(2) 和 (3)，我們得到：
$$\mathrm{\mathit{\frac{V_{\mathrm{1}}}{\mathrm{1}}\mathrm{\, =\, }\frac{V_{\mathrm{2}}}{\left ( \mathrm{1}\mathrm{\, +\, }K \right )}\mathrm{\, =\, }\frac{V_{\mathrm{3}}}{\left ( \mathrm{1\mathrm{\, +\, }3}K\mathrm{\, +\, }K^{\mathrm{2}} \right )}\mathrm{\, =\, }\frac{V}{\left ( \mathrm{1}\mathrm{\, +\, }K \right )\left ( \mathrm{3} \mathrm{\, +\, }K\right )} }\: \: \: \cdot \cdot \cdot \left ( 4 \right )}$$
因此，每個圓盤上的電壓由下式給出：
$\mathrm{頂部圓盤上的電壓,\mathit{V_{\mathrm{1}}\mathrm{\, =\, }\frac{V}{\left ( \mathrm{1}\mathrm{\, +\, }K \right )\left ( \mathrm{3} \mathrm{\, +\, }K\right )}}}$
$\mathrm{從頂部算起的第 2 個圓盤上的電壓,\mathit{V_{\mathrm{2}}\mathrm{\, =\, }\frac{V}{\left ( \mathrm{3} \mathrm{\, +\, }K\right )}\mathrm{\, =\, }V_{\mathrm{1}}\left ( \mathrm{1}\mathrm{\, +\, }K \right )}}$
$\mathrm{從頂部算起的第 3 個圓盤上的電壓,\mathit{V_{\mathrm{3}}\mathrm{\, =\, }V_{\mathrm{1}}\left ( \mathrm{1}\mathrm{\, +\, }\mathrm{3}K\mathrm{\, +\, }K^{\mathrm{2}} \right )}}$
因此，從上述數學分析可以觀察到以下幾點：
設K = 0.3，則根據公式 (4)，我們有V2 = 1.3 V1 和V3 = 1.99 V1。這表明最靠近導線的圓盤電壓最高。
K 的值越大，圓盤上的電壓分佈越不均勻，因此串的效率越低。
電位分佈的不均勻性隨著絕緣子串中圓盤數量的增加而增加。
5K+ 次檢視
