資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究路徑測試和基本路徑測試示例
基本路徑測試是一種基於程式或模組控制結構的白盒測試技術。使用此結構建立控制流圖，並使用此結構測試圖中的許多可能路徑。
識別控制流圖中提供程式或模組的基礎執行路徑集的路徑的方法稱為基本路徑測試。
由於此測試依賴於程式的控制結構，因此需要深入瞭解程式的結構。使用此技術建立測試用例遵循四個階段：
建立控制流圖。
計算圖的環路複雜度
識別未連線的路徑
基於獨立路徑建立測試用例。
控制流圖
控制流圖（或簡稱流圖）是一個有向圖，它描述了程式或模組的控制結構。控制流圖由 V 個節點/頂點和 E 個邊組成（V，E）。控制圖還可以包含以下內容：
有多個箭頭進入的節點稱為連線節點。
有多個箭頭離開的節點稱為決策節點。
邊和節點所包圍的區域稱為區域（圖外部的區域也計為一個區域）。
以下是構建流圖時使用的符號：
- 順序語句：
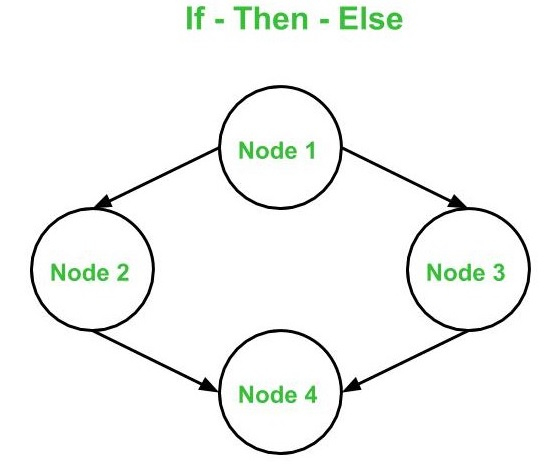
- 如果 - 則 - 否則
- 執行 - 直到
- 當 - 執行
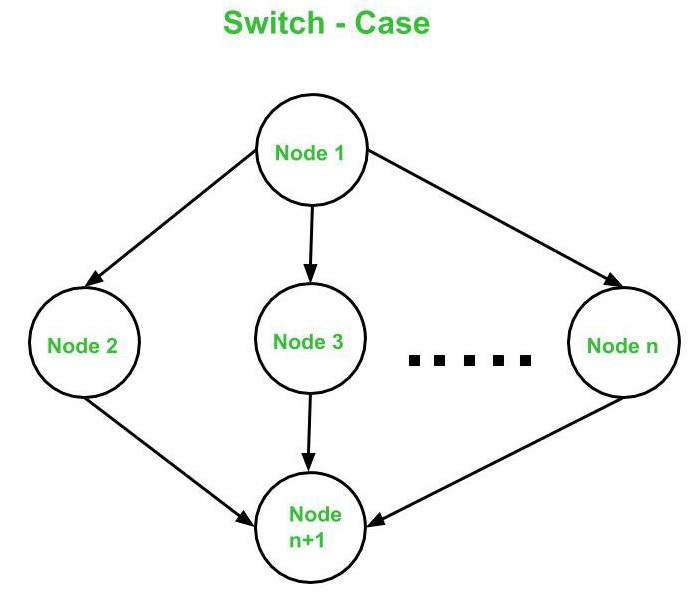
- 開關 - 案例
環路複雜度
環路複雜度 V(G) 被認為是程式邏輯複雜度的度量。可以使用三種不同的公式來計算它：
V(G) = e - n + 2*P 是基於邊和節點的公式。
其中 e 是邊的數量，n 表示頂點的數量，P 表示連線元件的數量。
例如，請參見上面顯示的第一個圖。
其中e = 4，n = 4，和p = 1都是整數
V(G) = 4 - 4 + 2 * 1 = 2 環路複雜度
以下是基於決策節點的公式：
V(G) = d + P，其中 d 表示決策節點的數量，P 表示連線節點的數量。
例如，請參見上面顯示的第一個圖。
其中d=1和p=1
V(G) = 1 + 1 = 2 環路複雜度
以下是基於區域的公式：
V(G) 表示圖中區域的數量。
例如，請參見上面顯示的第一個圖。
V(G) = 1（對於區域 1）+ 1（對於區域 2）= 2 環路複雜度
因此，使用所有三個公式得出的環路複雜度保持不變。這三個公式可用於計算和驗證流圖的環路複雜度。
觀察
每個函式[例如 Main( ) 或 Factorial() ]只建立一個流圖。如果程式中有多個函式，則為每個函式建立一個單獨的流圖。此外，環路複雜度公式中“p”的值由圖的總數決定。
如果正好有兩個箭頭離開決策節點，則將其計為一個決策節點。如果有多於兩個箭頭離開決策節點，則使用以下公式：
d = k - 1
k 表示離開決策節點的箭頭數。
獨立路徑
在控制流圖中，獨立路徑是指在建立路徑之前從未遍歷過的至少一條新邊的路徑。流圖的環路複雜度是存在的獨立路徑的數量。這是因為環路複雜度用作應執行測試次數的上限，以確保程式的所有語句至少執行一次。
在第一個圖中，獨立路徑的數量等於環路複雜度，因此獨立路徑的數量為 2。
因此，在上面提到的第一個圖中，獨立路徑為：
- A -> B 是第一條路徑。
- C 是第二條路徑。
注意：值得注意的是，獨立路徑不一定是唯一的。換句話說，如果圖的環路複雜度為 N，則有可能找到兩個不同的路徑集，每個路徑集本質上都是獨立的。
最後，一旦獲得單獨的路徑，就可以構造測試用例，每個測試用例表示一個或多個獨立路徑。
路徑測試示例
在之前的文章中，我們研究了使用基本路徑測試為程式建立測試用例所涉及的步驟。現在讓我們使用相同的步驟解決一個示例。
考慮以下程式，該程式確定一個整數是否為素數。以下是以下程式的時間表：
建立控制流圖。
使用所有可用方法計算迴圈複雜度。
列出所有獨立路徑設計測試用例。
int main (){
int n, index;
cout << "Enter a number: " << endl;
cin >> n;
index = 2;
while (index <= n - 1) {
if (n % index == 0) {
cout << "It is not a prime number" << endl;
break;
}
index++;
}
if (index == n)
cout << "It is a prime number" << endl;
} // end main解決方案：1. 建立控制流圖
步驟 1：在宣告變數後，開始對語句進行編號（如果該語句中沒有初始化變數）。但是，如果在同一行初始化和宣告變數，則應從該行開始編號。
以下是為提供的程式執行編號的方式：
int main (){
int n, index;
cout << "Enter a number: " <> n;
index = 2;
while (index <= n - 1){
if (n % index == 0){
cout << "It is not a prime number" << endl;
break;
}
index++;
}
if (index == n)
cout << "It is a prime number" << endl;
} // end main步驟 2：將所有順序語句合併到一個節點中。例如，語句 1、2 和 3 都是順序語句，應連線到一個節點中。對於其餘語句，我們將使用此處描述的符號。
注意：為簡單起見，按字母順序對節點進行編號。
生成的圖形如下所示：
使用以下公式計算環路複雜度：
方法 1
V(G) = e - n + 2*p
在上圖的控制流圖中，
其中 e = 10，n = 8，p =1
因此，V(G) = 10 - 8 + 2 * 1 = 4 環路複雜度
方法 2
V(G) = d + p
在上圖的控制流圖中，
其中 d = 3（節點 B、C 和 F）和 p = 1
因此，環路複雜度 V(G) = 3 + 1 = 4
方法 3
V(G) = 區域數（方法 3）
在上圖的控制流圖中，有四個區域，如下所示：
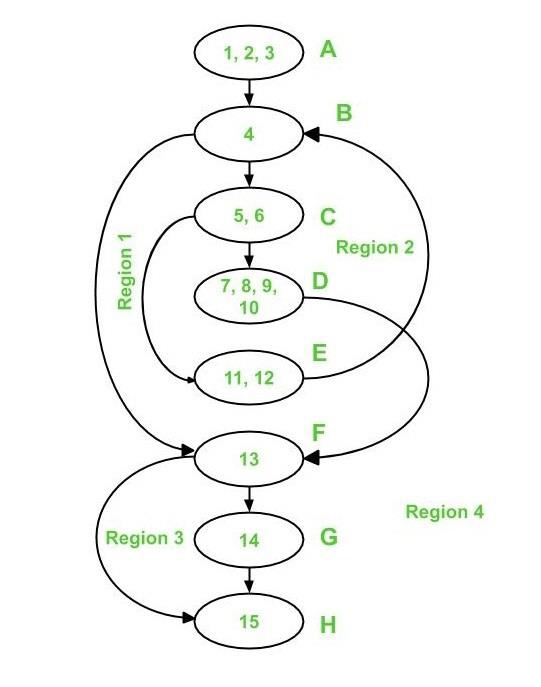
因此，有四個不同的區域：R1、R2、R3 和 R4。
V(G) = 1 + 1 + 1 + 1 = 4 環路複雜度
值得注意的是，所有三種方法都獲得相同的環路複雜度 V 值 (G)。
獨立路徑
由於圖的環路複雜度 V(G) 為 4，因此有 4 條獨立路徑。
路徑 1 覆蓋（紅色）以下邊：
A – B – F – G – H 是第一條路徑。
路徑 1 和路徑 2 覆蓋以下邊：
A – B – F – H 是第二條路徑。
路徑 1、路徑 2 和路徑 3 覆蓋以下邊：
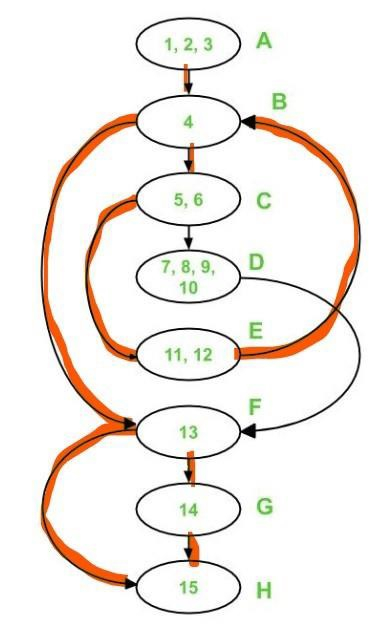
A - B - C - E - B - F - G - H 是第三條路徑
只有兩條邊未被覆蓋，即邊 C-D 和邊 D-F。因此，這兩條邊必須包含在路徑 4 中。
A - B - C - D - F - H 是第四條路徑。
這些路徑中的每條路徑都至少有一條以前從未遍歷過的新邊。
請注意，獨立路徑並不總是唯一的。
測試用例
我們必須使用先前發現的獨立路徑來生成測試用例。以這樣的方式向程式提供輸入，即執行每條獨立路徑以建立測試用例。
對於提供的程式，將獲得以下測試用例：
| 測試用例 ID | 輸入數字 | 輸出 | 覆蓋的獨立路徑 |
|---|---|---|---|
| 1 | 1 | 無輸出 | A-B-F-H |
| 2 | 2 | 它是一個素數 | A-B-F-G-H |
| 3 | 3 | 它是一個素數 | A-B-C-E-B-F-G-H |
| 4 | 4 | 它不是一個素數 | A-B-C-D-F-H |
基本路徑測試的優點
基本路徑測試在以下情況下很有用：
額外覆蓋率：因為它側重於最大邏輯覆蓋率而不是最大路徑覆蓋率，所以基本路徑測試提供了最佳的程式碼覆蓋率。因此，程式碼總體上得到了很好的測試。
維護測試：當修改軟體的一部分時，仍然需要測試所做的更改，這需要路徑測試。
當開發人員生成程式碼時，他或她首先要做的是測試程式或模組的結構。因此，基本路徑測試需要深入瞭解程式碼的結構。
整合測試：當一個模組呼叫另一個模組時，存在相當大的介面問題風險。路徑測試用於測試模組介面上的所有路徑，以避免此類問題。
測試工作量：由於軟體（即程式或模組）的環路複雜度是使用基本路徑測試技術計算的，因此很明顯可以觀察到，基本路徑測試中的測試工作量與軟體或程式的複雜度直接相關。
19K+ 次瀏覽
