Python Wand 中的 path_curve_to_quadratic_bezier() 函式
貝塞爾曲線是 Python 的內建繪圖函式。它用於根據給定的點在 Python 中繪製曲線。
二次貝塞爾曲線是一個 Python 函式,它透過頂點(控制點)為二次貝塞爾曲線繪製路徑。二次貝塞爾曲線是一個引數曲線,它定義了二維空間中的路徑。該曲線由一個控制點和兩個端點連線。
在視覺化程式中,您可以使用此函式輕鬆構建和繪製。使用時間引數,您可以找到兩個控制點並確定它們的位置。您可以透過這種方式構建敏感位置並將這些位置像曲線一樣連線起來。藉助此函式,我們可以輕鬆建立使用其他函式或方法難以或無法建立的曲線和形狀。例如,藉助二次貝塞爾函式,我們可以建立不同型別的圖表和動畫。
語法
此語法用於給定的示例:
def quadratic_bezier(p0, p1, p2, t):
這裡 p0、p1 和 p2 代表點,t 代表值。
示例 1
在這個程式中,我們使用不同的點繪製曲線。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (0, 3) # beginning point
p1 = (4, 2) # Control point
p2 = (1, 8) # finishing point
t = 50
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
輸出
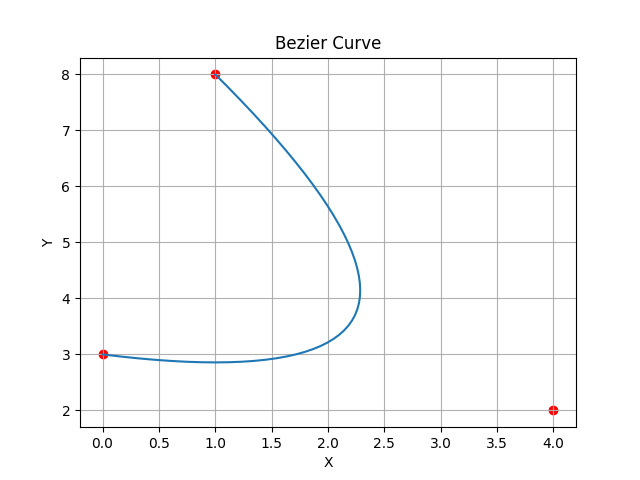
在此程式碼中,我們使用 matplotlib 和 numpy 建立了一個貝塞爾曲線。我們已定義並使用它來繪製在貝塞爾曲線上執行的點。起始點、控制點和結束點將顯示在輸出中。
示例 2
在這個程式中,我們使用不同的點繪製曲線。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (2, 3) # beginning point
p1 = (6, 5) # Control point
p2 = (3, 2) # finishing point
t = 50
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
輸出
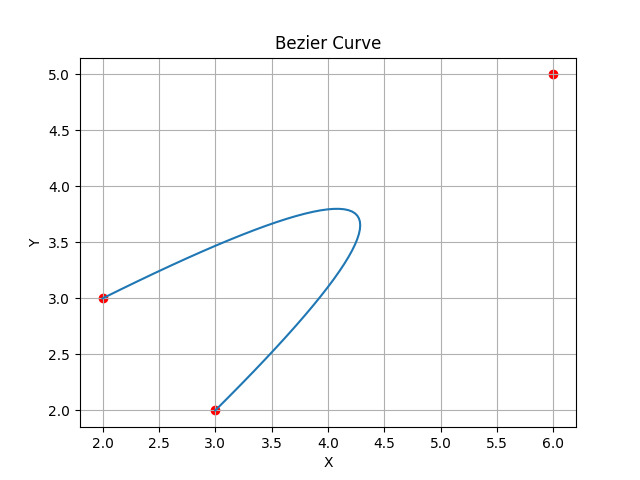
在此程式碼中,我們使用 matplotlib 和 numpy 生成了一個貝塞爾曲線。我們使用的方法定義並繪製了貝塞爾曲線上起始的點。輸出將顯示起始點、控制點和結束點。
示例 3
在這個程式中,我們使用不同的點繪製曲線。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (2, 3) # beginning point
p1 = (-2, 5) # Control point
p2 = (-3, 2) # finishing point
t = 80
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
輸出
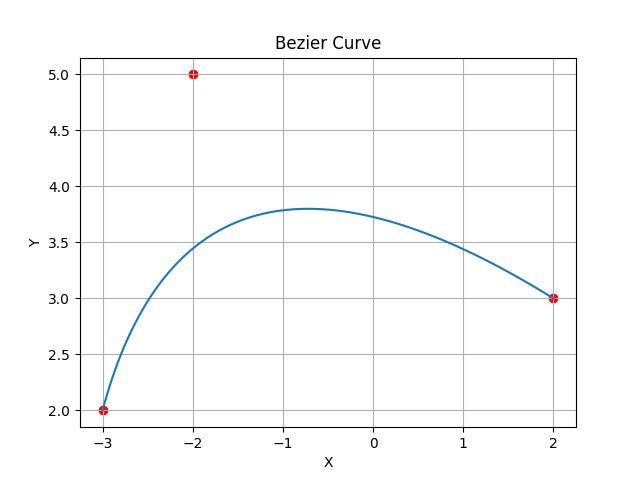
在此程式碼中,為了建立貝塞爾曲線,使用了 matplotlib 和 numpy。我們使用的方法定義並繪製了貝塞爾曲線上起始的點。輸出或圖表中將顯示起始點、控制點和結束點。
示例 4
在這個程式中,我們使用不同的點繪製曲線。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (2, -5) # beginning point
p1 = (-2, 5) # Control point
p2 = (-3, 2) # finishing point
t = 50
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
輸出
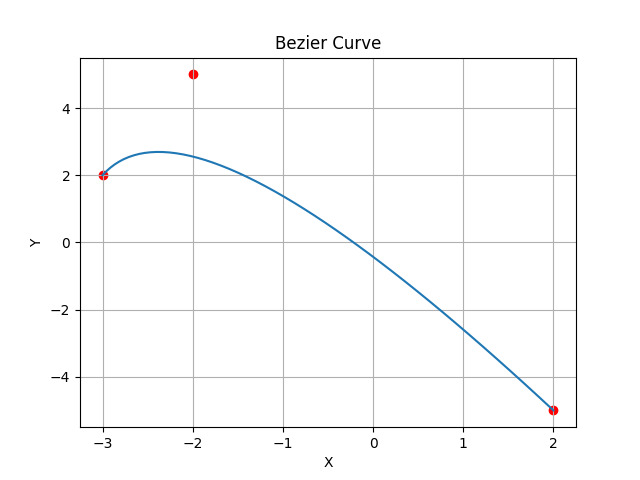
在此程式碼中,使用 matplotlib 和 numpy,我們構建了一個貝塞爾曲線。我們已經識別並使用了沿貝塞爾曲線的點。影像將顯示起始點、控制點和結束點。
在上面的示例中,我們可以看到透過使用起始點、控制點和結束點建立的不同圖表。
結論
總之,二次貝塞爾函式用於 Python Wand 建立平滑曲線。它需要三個點作為輸入,並生成一條透過端點並受控制點位置影響的曲線。


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP