一對一函式

---

介紹

一對一函式是指將值域的每個元素對映到其定義域中的一個元素的函式。函式定義為一組輸入與其各自輸出之間的關係。簡單來說，函式是輸入之間的關係，其中每個輸入都與一個輸出相關聯。每個函式都有一個定義域和一個陪域或值域。函式通常用𝑓(𝑥)表示，其中x是輸入。

函式的一般表示形式為

$$\mathrm{y\:=\:f(x)}$$

從數學角度來看，這些關係可以描述為一對一函式。在這種情況下，元素的數量相同，或者一個元素只能與另一個元素配對。

在本教程中，我們將討論一對一函式。

函式

函式是一種特殊的關係。數學函式通常被視為給出每個輸入x的唯一輸出的規則。對映或變換用於表示數學函式。這些函式通常用f、g和h等字母表示。定義域定義為您可以輸入的所有值的集合，而函式可以被定義。值域包含作為問題中函式輸出返回的所有值。陪域是一組可以作為函式輸出輸出的值。

每個函式都有一個定義域和一個陪域或值域。函式通常用𝑓(𝑥)表示，其中x是輸入。

函式的一般表示形式為

$$\mathrm{y\:=\:f(x)}$$

函式型別

基於集合元素的不同型別的函式：

• 一對一函式

• 多對一函式

• 滿射函式

• 一對一且滿射函式

• 入射函式

• 常數函式

一對一函式

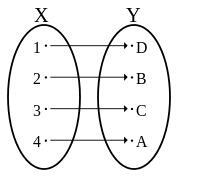
術語“一對一關係”實際上指的是任何兩個物件之間的關係，其中一個物件只能與另一個物件相關聯。從數學角度來看，這些關係可以描述為一對一函式。在這種情況下，元素的數量相同，或者一個元素只能與另一個元素配對。

多對一函式

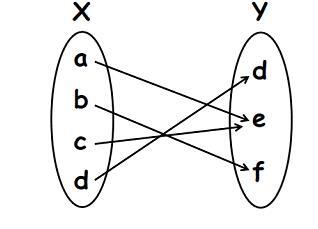
多對一函式由函式$\mathrm{f\:\colon\:A\rightarrow\:B}$定義，使得集合A的多個元素連線到集合B的相同元素。對於多對一特性，多個元素共享相同的陪域或像。如果陪域多對一函式只有一個值。

滿射函式

在滿射函式中，每個陪域元素都與定義域元素相關聯。對於在A→B中定義的函式，集合B中的所有元素都具有集合A的原像。滿射函式也稱為滿射函式。

一對一且滿射函式

既是一對一函式又是滿射函式的函式稱為雙射函式。在這裡，定義域的每個元素都對映到陪域內的特定元素，並且陪域的每個元素都有一個原型（原像）。也就是說，集合A中的所有元素都與集合B中的特定元素相關聯，集合B中沒有剩餘元素。

入射函式

就其屬性而言，入射函式與滿射函式完全相反。這裡，末尾有一個特定的元素沒有原像（原型）。集合B的元素是冗餘的，並且與集合A的任何元素都不相關聯。

常數函式

這些函式是多對一函式的一種重要形式。在常數函式中，每個定義域元素都只有一個像。

常數函式的格式為f(x) = K，其中K是一個實數。對於常數函式中不同值域的值（x值），獲取相同值域中的K值。

一對一（單射）函式

一對一（單射）函式是一種特殊的函式，它將值域的每個元素精確地對映到其定義域中的一個元素，即輸出不會重複。一對一函式由f: X → Y定義，使得集合X的每個元素都與集合Y的特定元素相關聯。一對一函式也稱為單射函式。在這裡，定義域的每個元素都有一個特定於特定函式的像或陪域元素。“一對一關係”一詞實際上指的是任何兩個物件之間的關係，其中一個物件只能與另一個物件相關聯。從數學角度來看，這些關係可以描述為一對一函式。在這種情況下，元素的數量相同，或者一個元素只能與另一個元素配對。

如何證明一個函式是一對一的

1. 證明函式是一對一或滿射的最佳方法是使用定義。

如果對於每個𝑥, 𝑦 ∈ 𝐴，$\mathrm{f(x)\:=\:f(y)\:then\:x\:=\:y}$，則函式𝑓: 𝐴 → 𝐵被稱為一對一（單射）函式。

這僅僅意味著A的唯一元素對映到B的唯一元素。讓我們來看一下定義為$\mathrm{f(x)\:=\:2x\:+\:4}$的函式𝑓: 𝑅 → 𝑅。

現在我們需要證明它是一對一函式。

假設$\mathrm{f(x)\:=\:f(y)}$

這意味著$\mathrm{2x\:+\:4\:=\:2y\:+\:4}$

或$\mathrm{x\:=\:y}$

因此，根據定義，f(x)是一對一函式。

2. 水平線檢驗。

單射函式可以透過水平線檢驗或幾何檢驗來確定。如果水平線只與函式圖相交一次，則該函式是一對一的。

如果水平線與函式圖相交多次，則該函式不是一對一的。

已解決的例子

1) 證明定義為$\mathrm{f(x)\:=\:6x\:+\:9}$的函式$\mathrm{f\colon\:R\rightarrow\:R}$是單射函式或一對一函式。

答案：給定定義為$\mathrm{f(x)\:=\:6x\:+\:9}$的函式$\mathrm{f\colon\:R\rightarrow\:R}$

現在我們需要證明它是一對一函式。

假設$\mathrm{f(x)\:=\:f(y)}$

這意味著$\mathrm{6x\:+\:9\:=\:6y\:+\:9}$

或$\mathrm{x\:=\:y}$

因此，根據定義，f(x)是一對一函式。

2) 如果𝑨 = {4, 5, 6}並且𝑩 = {p, q, r, s}，則以下哪個函式是一對一的。

$\mathrm{\lbrace\:(4\:,\:r)\:,\:(5\:,\:r)\:,\:(5\:,\:r)\rbrace\:}$

$\mathrm{\lbrace\:(4\:,\:p)\:,\:(5\:,\:r)\:,\:(6\:,\:s)\rbrace\:}$

$\mathrm{\lbrace\:(4\:,\:p)\:,\:(4\:,\:r)\rbrace\:}$

答案 - {(4, p),(5, r),(6, s)} 這是一個一對一函式。這是因為集合B的元素唯一地對映到集合A的元素。

3) 證明定義為$\mathrm{f(x)\:=\:x^{2}\:-\:2}$的函式$\mathrm{f\colon\:R\rightarrow\:R}$不是一對一函式。

答案 - 對於一對一函式$\mathrm{f(x)\:=\:f(y)}$

$$\mathrm{x^{2}\:-\:2\:=\:y^{2}\:-\:2}$$

$$\mathrm{\Longrightarrow\:x^{2}\:=\:y^{2}}$$

$$\mathrm{\:\:\:\:\:\:\:\:\Longrightarrow\:x^{2}\:-\:y^{2}\:=\:0}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:(x\:-\:y)\:(x\:+\:y)\:=\:0}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:x\:=\:y\:and\:x\:=\:-y}$$

由於我們在x和y中得到了兩個關係𝑥 = 𝑦 𝑎𝑛𝑑 𝑥 = −𝑦，因此它不滿足一對一函式的條件。

結論

術語“一對一關係”實際上指的是任何兩個物件之間的關係，其中一個物件只能與另一個物件相關聯。從數學角度來看，這些關係可以描述為一對一函式。在這種情況下，元素的數量相同，或者一個元素只能與另一個元素配對。

常見問題

1. 函式是什麼意思？

函式是一種特殊的關係。數學函式通常被視為給出每個輸入x的唯一輸出的規則。

2. 一對一函式是什麼意思？

術語“一對一關係”實際上指的是任何兩個物件之間的關係，其中一個物件只能與另一個物件相關聯。

3. 滿射函式是什麼意思？

在滿射函式中，每個陪域元素都與定義域元素相關聯。對於在A→B中定義的函式，集合B中的所有元素都具有集合A的原像。滿射函式也稱為滿射函式。

4. 一對一且滿射函式是什麼意思？

既是一對一函式又是滿射函式的函式稱為雙射函式。在這裡，定義域的每個元素都對映到陪域內的特定元素，並且陪域的每個元素都有一個原型（原像）。

5. 多對一函式是什麼意思？

多對一函式由函式$\mathrm{f\colon\:A\rightarrow\:B}$定義，使得集合A的多個元素連線到集合B的相同元素。對於多對一特性，多個元素共享相同的陪域或像。