資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究使用 C++ 程式中的動態規劃查詢二叉樹中節點的最大和，且這些節點互不相鄰
在這個問題中，我們給定一個二叉樹，每個節點都有一個值。我們的任務是建立一個程式，使用動態規劃查詢二叉樹中節點的最大和，且這些節點互不相鄰。
問題描述 − 我們將選擇二叉樹的子集，使和最大化，並且這些節點不能直接連線。
讓我們舉個例子來理解這個問題，
輸入
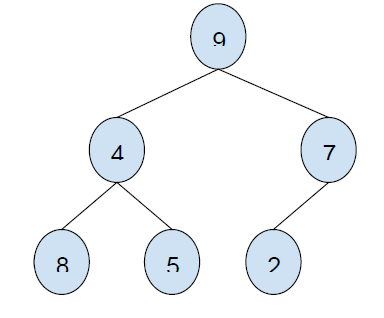
輸出
24
解釋
Elements to be taken under consideration are: 8 + 5 + 9 + 2 = 24
解決方案方法
解決此問題的方法是使用對映並找到節點的總和，使得它們形成 maxSum。根據給定的條件，節點及其子節點都不能
考慮在總和中。因此，我們需要在考慮節點之前檢查其子樹是否包含構成更大總和的某些元素。
對於每個節點，多次查詢相同父-子子樹的總和會增加計算開銷，為了解決這個問題，我們將使用記憶化並將節點的 maxSum 儲存在對映中，以便以後使用。
示例
程式說明了我們解決方案的工作原理，
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
struct node *left, *right;
};
struct node* newNode(int data){
struct node *temp = new struct node;
temp−>data = data;
temp−>left = temp−>right = NULL;
return temp;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum);
int sumSubTreeNodes(node* node, map<struct node*, int>& nodeSum){
int maxSum = 0;
if (node−>left)
maxSum += findMaxSumBT(node−>left−>left, nodeSum) +
findMaxSumBT(node−>left−>right, nodeSum);
if (node−>right)
maxSum += findMaxSumBT(node−>right−>left, nodeSum) +
findMaxSumBT(node−>right−>right, nodeSum);
return maxSum;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum){
if (node == NULL)
return 0;
if (nodeSum.find(node) != nodeSum.end())
return nodeSum[node];
int sumInclCurr = node−>data + sumSubTreeNodes(node, nodeSum);
int sumExclCurr = findMaxSumBT(node−>left, nodeSum) +
findMaxSumBT(node−>right, nodeSum);
nodeSum[node] = max(sumInclCurr, sumExclCurr);
return nodeSum[node];
}
int main(){
node* root = newNode(9);
root−>left = newNode(4);
root−>right = newNode(7);
root−>left−>left = newNode(8);
root−>left−>right = newNode(5);
root−>right−>left = newNode(2);
map<struct node*, int> nodeSum;
cout<<"Maximum sum of nodes in Binary tree such that no two are
adjacent using Dynamic Programming is "<<findMaxSumBT(root,
nodeSum);
return 0;
}輸出
Maximum sum of nodes in Binary tree such that no two are adjacent using Dynamic Programming is 24
更新於: 2020-12-09
382 次檢視
廣告