資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律學在美國和加拿大等國家，溫度使用華氏度進行測量，而在印度等國家，則使用攝氏度進行測量。以下是一個將華氏度轉換為攝氏度的線性方程
\[\mathrm{F}=\left(\frac{9}{5}\right) \mathrm{C}+32
\]
(i) 使用攝氏度作為x軸，華氏度作為\( y \)軸，繪製上述線性方程的圖形。
(ii) 如果溫度是\( 30^{\circ} \mathrm{C} \)，華氏度是多少？
(iii) 如果溫度是\( 95^{\circ} \mathrm{F} \)，攝氏度是多少？
(iv) 如果溫度是\( 0^{\circ} \mathrm{C} \)，華氏度是多少？如果溫度是\( 0^{\circ} \mathrm{F} \)，攝氏度是多少？
(v) 是否存在一個溫度在華氏度和攝氏度下數值相同？如果存在，請找出這個溫度。
已知
將華氏度轉換為攝氏度的線性方程為
$F=(\frac{9}{5})C+32$。
解題步驟
我們需要找到給定問題的解。
解答
已知：
$F=(\frac{9}{5})C+32$
(i) 以攝氏度為x軸，華氏度為y軸，在圖上繪製線性方程。
我們知道：
要繪製一個二元線性方程的圖形，我們需要至少兩個解。
為了找到給定方程$F=(\frac{9}{5})C+32$的解。
讓我們在方程$F=(\frac{9}{5})C+32$中代入$C=0$
對於$C=0$
我們得到：
$F=(\frac{9}{5})0+32$
$F=32$
對於$C=-10$
我們得到：
$F=(\frac{9}{5})(-10)+32$
$F=9(-2)+32$
$F=-18+32$
$F=14$
因此，
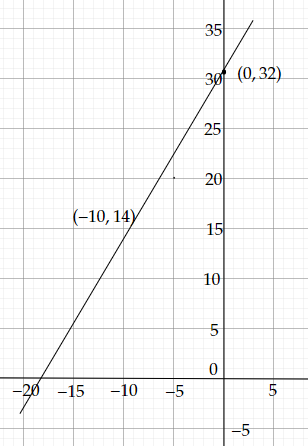
$(0, 32)$ 和 $(-10, 14)$ 是方程$F=(\frac{9}{5})C+32$的兩個解。
因此，
二元線性方程$F=(\frac{9}{5})C+32$的圖形是，(此處應插入圖形)
(ii) 溫度為$30^o\ C$，
這意味著：
$C=30$
將$C$代入線性方程$F=(\frac{9}{5})C+32$
我們得到：
$F=(\frac{9}{5})30+32$
$F=9(6)+32$
$F=54+32$
$F=86$
因此，華氏度溫度為$86^o$。
(iii) 溫度為$95^oF$
這意味著：
$F = 95$
將$F$代入線性方程$F=(\frac{9}{5})C+32$
我們得到：
$95=(\frac{9}{5})C+32$
$(\frac{9}{5})C=95-32$
$(\frac{9}{5})C=63$
$C=\frac{63\times5}{9}$
$C=35$
因此，攝氏度溫度為$35^o$。
(iv) 溫度為$0^o\ C$，
這意味著：
$C=0$
將$C$代入線性方程$F=(\frac{9}{5})C+32$
我們得到：
$F=(\frac{9}{5})0+32$
$F=0+32$
$F=32$
因此，華氏度溫度為$32^o$。
溫度為$0^oF$
這意味著：
$F = 0$
將$F$代入線性方程$F=(\frac{9}{5})C+32$
我們得到：
$0=(\frac{9}{5})C+32$
$(\frac{9}{5})C=-32$
$C=\frac{-32\times5}{9}$
$C=-17.777$
$C≈-17.8$
因此，攝氏度溫度為$-17.8^o$。
(v) 華氏度和攝氏度數值相同的溫度
這意味著：
$F=C$
$C=(\frac{9}{5})C+32$
$C-(\frac{9}{5})C=32$
$\frac{(5-9)C}{5}=32$
$(\frac{-4}{5})C=32$
$C=\frac{-32\times5}{4}$
$C=-40$
因此，
華氏度和攝氏度數值相同的溫度為$-40^o$。
瀏覽量：87
