資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝學
法學在 C++ 中查詢平衡 BST 中是否存在三元組加起來等於零
假設我們有一個平衡的二叉搜尋樹，我們需要建立一個名為 `is_valid_triplet()` 的函式，當給定 BST 中存在一個三元組的和等於 0 時返回 `true`，否則返回 `false`。請根據以下約束設計此方法：
預期時間複雜度為 O(n^2)
可以使用 O(logn) 的額外空間。
因此，如果輸入如下所示：
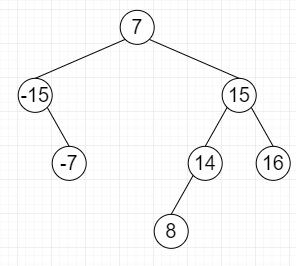
則輸出將為 True，因為三元組為 [-15,7,8]
為了解決這個問題，我們將遵循以下步驟：
定義一個函式 `bst_to_doubli_list()`，它將接收根節點、頭節點和尾節點。
如果根節點為空，則：
返回
如果根節點的左子節點不為空，則：
bst_to_doubli_list(根節點的左子節點, 頭節點, 尾節點)
根節點的左子節點 := 尾節點
如果尾節點不為空，則：
尾節點的右子節點 := 根節點
否則
頭節點 := 根節點
尾節點 := 根節點
如果根節點的右子節點不為空，則：
bst_to_doubli_list(根節點的右子節點, 頭節點, 尾節點)
定義一個函式 `is_in_double_list()`，它將接收頭節點、尾節點和總和。
當頭節點不等於尾節點時，執行以下操作：
當前值 := 頭節點的值 + 尾節點的值
如果當前值等於總和，則：
返回 true
否則，如果當前值 > 總和，則：
尾節點 := 尾節點的左子節點
否則
頭節點 := 頭節點的右子節點
返回 false
在主方法中，執行以下操作：
如果根節點為空，則：
返回 false
頭節點 = 空
尾節點 = 空
bst_to_doubli_list(根節點, 頭節點, 尾節點)
當 (頭節點的右子節點不等於尾節點且頭節點的值 < 0) 時，執行以下操作：
如果 is_in_double(頭節點的右子節點, 尾節點, 頭節點的值 * (-1))，則
返回 true
否則
頭節點 := 頭節點的右子節點
返回 false
示例 (C++)
讓我們看看下面的實現，以便更好地理解：
#include <bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int key;
TreeNode *left;
TreeNode *right;
TreeNode() : key(0), left(NULL), right(NULL) {}
TreeNode(int x) : key(x), left(NULL), right(NULL) {}
};
void bst_to_doubli_list(TreeNode* root, TreeNode** head, TreeNode** tail) {
if (root == NULL)
return;
if (root->left)
bst_to_doubli_list(root->left, head, tail);
root->left = *tail;
if (*tail)
(*tail)->right = root;
else
*head = root;
*tail = root;
if (root->right)
bst_to_doubli_list(root->right, head, tail);
}
bool is_in_double_list(TreeNode* head, TreeNode* tail, int sum) {
while (head != tail) {
int current = head->key + tail->key;
if (current == sum)
return true;
else if (current > sum)
tail = tail->left;
else
head = head->right;
}
return false;
}
bool is_valid_triplet(TreeNode *root) {
if (root == NULL)
return false;
TreeNode* head = NULL;
TreeNode* tail = NULL;
bst_to_doubli_list(root, &head, &tail);
while ((head->right != tail) && (head->key < 0)){
if (is_in_double_list(head->right, tail, -1*head->key))
return true;
else
head = head->right;
}
return false;
}
TreeNode* insert(TreeNode* root, int key) {
if (root == NULL)
return new TreeNode(key);
if (root->key > key)
root->left = insert(root->left, key);
else
root->right = insert(root->right, key);
return root;
}
int main(){
TreeNode* root = NULL;
root = insert(root, 7);
root = insert(root, -15);
root = insert(root, 15);
root = insert(root, -7);
root = insert(root, 14);
root = insert(root, 16);
root = insert(root, 8);
cout << is_valid_triplet(root);
}輸入
root = insert(root, 7); root = insert(root, -15); root = insert(root, 15); root = insert(root, -7); root = insert(root, 14); root = insert(root, 16); root = insert(root, 8);
輸出
1
159 次瀏覽
