資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學FIFO 推入重標記演算法
FIFO 推入重標記演算法是一種用於解決最大流問題的演算法。
最大流問題是圖論中的一個問題，我們需要找到可以透過互連的元件網路（例如管道、電線等）傳送的資源或資訊的最大流量，同時受到單個元件能夠處理的容量限制。
換句話說，我們有一個 N 個節點的有向圖。我們給定一個源節點和一個匯點。圖中還有 M 條邊，每條邊都有一個權重，表示它能夠處理的最大容量。我們需要找出可以在不超過任何邊的容量的情況下從源節點傳輸到匯點的最大流量。
在第一種方法中，我們給定一個有向圖 G，表示流量網路的邊。每條邊都有一個權重，表示該邊的最大容量。我們最初將每條邊的流量初始化為零。我們反覆檢查是否可以透過廣度優先搜尋將資訊從源節點傳輸到匯點。只要有辦法將資訊從源節點傳輸到匯點，我們就傳輸該資訊量並將其新增到最終答案中。我們還從所涉及的每條邊的容量中減去它。
問題陳述
給定一個以有向圖 G 形式表示的流量網路，以及表示每條邊最大容量的邊權重。我們需要找到可以從源節點傳輸到匯點的最大流量，條件是：
沒有邊的負載超過其容量。
到達一個節點的所有入邊之和等於所有出邊之和。
示例
輸入
Source = 1, Sink = 4
輸出
10
解釋
我們可以從 1 流到 2 共 10 個單位，由於入邊和出邊必須具有相同的和，我們只能從 2 移動到 3 共 10 個單位，同樣從 3 移動到 4 共 10 個單位。
輸入
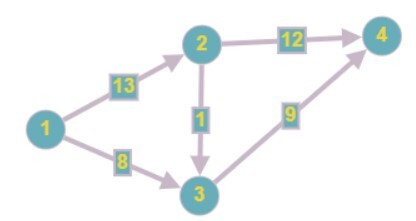
Source = 1, Sink = 4
輸出
21
解釋
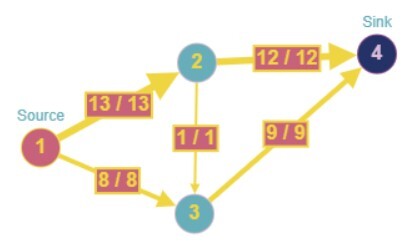
輸入
Source = 1, Sink = 6
輸出
23
解釋
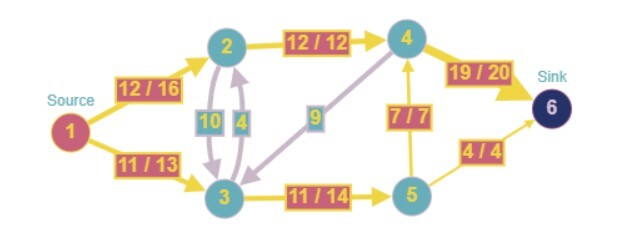
如上圖所示，我們可以獲得 23 的最大流量。
由於入邊之和必須等於出邊之和，並且頂點 4 的入邊之和為 19，我們只能從邊 4-6 流動 19 個單位，即使邊的容量為 20。
方法
在這種方法中，我們給定一個有向圖 G，表示流量網路的邊。每條邊都有一個權重，表示該邊的最大容量。我們最初將每條邊的流量初始化為零。我們反覆檢查是否可以透過廣度優先搜尋將資訊從源節點傳輸到匯點。只要有辦法將資訊從源節點傳輸到匯點，我們就傳輸該資訊量並將其新增到最終答案中。我們還從所涉及的每條邊的容量中減去它。
演算法
步驟 1.1 − 將所有邊的初始流量設定為零。
步驟 1.2 − 為源節點分配一個等於網路中節點總數的高度。
步驟 1.3 − 計算源節點的剩餘流量，即從源節點發出的所有邊的容量之和。
步驟 2.1 − 在每個節點（不包括源節點和匯點）處，檢查是否存在超過入流的剩餘流量，以及是否存在高度比當前節點高度低一個單位的相鄰節點。
步驟 2.2 − 如果上述條件為真，則沿邊儘可能多地推送流量，並更新當前節點的剩餘流量和邊的總容量。
步驟 3.1 − 如果上述條件為假，則需要增加該節點的高度。
步驟 3.2 − 透過在其當前容量大於零的相鄰節點的最小高度上加一來計算節點的新高度。
步驟 4.1 − 該演算法使用先進先出 (FIFO) 佇列來系統地管理要處理的節點，而不是反覆掃描所有節點以查詢潛在的推送和重標記。
步驟 4.2 − 檢查步驟 2.1 中提到的條件後，我們將相鄰節點推入佇列。
步驟 5 − 該演算法執行直到網路中沒有節點從源節點獲得任何剩餘流量。滿足此條件後，演算法返回最大流量。
示例
#include <bits/stdc++.h>
using namespace std;
bool Can_push(vector<vector<int>> &Capacity, int source, int sink, vector<int> &parent) {
int N = Capacity.size();
vector<int> vis(N,0);
vis[source]=1;
parent[source]=-1;
queue<int> que;
que.push(source);
while(!que.empty()) {
int cnode = que.front();
que.pop();
for (int i=0;i<N;i++){
if (vis[i]==0 && Capacity[cnode][i] > 0){
vis[i] = 1;
parent[i] = cnode;
que.push(i);
}
}
}
if(vis[sink])return true;
return false;
}
int FIFOPushRelabel(vector<vector<int>> &Capacity, int source, int sink){
int N = Capacity.size();
vector<int> parent(N);
int max_flow = 0;
while(Can_push(Capacity,source,sink,parent)){
int curr_flow = INT_MAX;
int temp = sink;
while(temp!=source){
curr_flow = min(curr_flow,Capacity[parent[temp]][temp]);
temp = parent[temp];
}
temp = sink;
while(temp!=source){
Capacity[parent[temp]][temp]-=curr_flow;
temp = parent[temp];
}
max_flow+=curr_flow;
}
return max_flow;
}
int main() {
vector<vector<int>> Capacity = {
{0, 16, 13, 0, 0, 0},
{0, 0, 10, 12, 0, 0},
{0, 4, 0, 0, 14, 0},
{0, 0, 9, 0, 0, 20},
{0, 0, 0, 7, 0, 4},
{0, 0, 0, 0, 0, 0}
};
int source = 0, sink = 5;
cout<<FIFOPushRelabel(Capacity,source,sink);
return 0;
}
輸出
23
時間複雜度 − O(V^3)，其中 V 是圖中節點的數量。
空間複雜度 − O(V^2)，用於儲存表示圖的鄰接矩陣。
197 次檢視
