光學顯微鏡和電子顯微鏡的區別

---

簡介

藉助我們的眼睛，我們可以看到我們周圍美麗的自然世界。這是由於光線的作用。光線照射到任何物體上並被反射。這些反射光線進入我們的眼睛。眼睛有很多部分，比如角膜、房水和晶狀體。從這裡發出的光以電訊號的形式透過視神經傳到大腦。

但是，有些物體我們用肉眼無法看清。我們發現用眼睛很難看清遙遠的行星和恆星。此外，像細胞、病毒或原子這樣的小物體也無法用肉眼看到。因此，為了觀察這些物體，我們需要藉助一些儀器。這些被稱為光學儀器。放大鏡就是一個常見的例子。我們可以將它們分為兩類——一類用於觀察遠處的物體，另一類用於觀察微小的物體。

用於觀察小物體或微小物體的裝置稱為顯微鏡。儘管有許多種類的顯微鏡，但在接下來的章節中，我們將學習光學顯微鏡和電子顯微鏡。

什麼是光學顯微鏡？

它是一種使用可見光波的顯微鏡。這意味著光波從我們想要觀察的物體上反射，然後進入我們的眼睛。最後，我們就能看到物體的放大影像。它也被稱為光學顯微鏡。在這種顯微鏡中，我們使用可見光，波長在 400-700 奈米之間。

我們可以使用這種望遠鏡中的透鏡進行放大。只有一個透鏡的顯微鏡稱為簡單顯微鏡。複合顯微鏡有兩個透鏡。

光學顯微鏡的構造和工作原理

簡單顯微鏡和複合顯微鏡是兩種不同型別的顯微鏡。

• 簡單顯微鏡 - 它由一個位於物體和眼睛之間的凸透鏡組成。凸透鏡放大物體，我們看到一個更大的影像。這是放大鏡和目鏡中使用的顯微鏡。

• 複合顯微鏡 - 在這種顯微鏡中，使用兩個凸透鏡。靠近物體的透鏡稱為物鏡。它產生物體的實像。此影像形成在顯微鏡內部（影像 1）。靠近眼睛的透鏡會產生此實像的放大影像（影像 2）。此透鏡稱為目鏡。

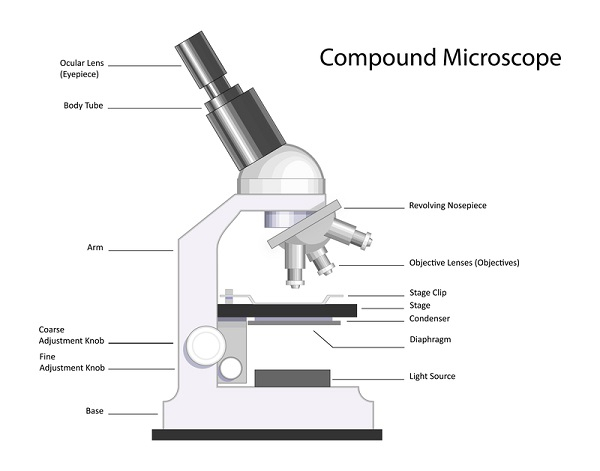
光學顯微鏡的優缺點

優點	缺點
使用非常簡單，便於攜帶	解析度低
不受電磁輻射的影響	無法提供 3D 影像
允許用於活生物體	放大倍數不大
維護成本非常低	無法在黑暗中操作

什麼是電子顯微鏡？

在電子顯微鏡中，我們使用電子束而不是可見光作為照明。如果我們使用電子束，則它們的波長大約比可見光的波長小 104 倍。因此，它比光學顯微鏡具有更高的解析度。它不僅可以提供物體的影像，還可以告訴我們物體的結構。以下是一些主要的電子顯微鏡型別

• 透射電子顯微鏡

• 掃描電子顯微鏡

• 反射電子顯微鏡

• 掃描隧道顯微鏡

電子顯微鏡的構造和工作原理

電子顯微鏡的主要部件如下：

• 電子槍 - 這裡使用鎢絲，加熱時會發射電子。

• 電磁透鏡 - 使用聚光鏡、物鏡和投影鏡。

• 載物臺 - 由非常薄的碳片製成。

• 成像系統 - 相機位於熒光屏下方

電子槍用作電子源。第一個聚光鏡將電子束聚焦到物體上，然後第二個聚光鏡用於形成細電子束。反射後從物體發出的電子透過稱為物鏡的磁線圈。然後從投影鏡獲得最終影像。影像可以在熒光屏上看到。

電子顯微鏡的優缺點

優點	缺點
提供非常高的放大倍數	電子束會殺死活生物體
也可以建立 3D 影像	使用起來並不容易
高解析度	電磁場的存在會影響影像。

結論

光學顯微鏡和電子顯微鏡都用於放大微小的物體。但是，它們之間存在一些差異。在光學顯微鏡中，我們使用可見光，而在電子顯微鏡中，使用電子束。電子顯微鏡的放大倍數和解析度高於光學顯微鏡。

常見問題

Q1. 放大倍數是肉眼看到的物體高度與使用透鏡後看到的物體高度之比。

答：$$\mathrm{m=\frac{h^{'}}{h}}$$

對於簡單顯微鏡，放大倍數由下式給出：

$$\mathrm{m=1+\frac{D}{f}}$$

這裡 D = 最近清晰視覺距離。

f= 透鏡的焦距

Q2. 電子顯微鏡有哪些應用？

答：電子顯微鏡廣泛應用於以下領域

• 在醫學領域，用於活檢樣本和細胞研究等。

• 在工業中，它用於質量控制

• 晶體學家用它來研究晶體的內部結構。

• 在生物學中，它用於研究病毒、細菌等微生物。

Q3. 寫出光學顯微鏡和電子顯微鏡的主要區別。

答：

光學顯微鏡	電子顯微鏡
使用光作為照明	使用電子束作為照明
可以觀察活的或死的物體	主要用於死亡和乾燥的樣本
放大倍數是原始尺寸的 500 到 1500 倍	放大倍數是原始尺寸的 100000 到 300000 倍
物體的影像是有色的	物體的影像是黑白的
待研究的樣品可在幾分鐘內製備好	待研究樣品的製備時間可能需要幾天。

Q4. 掃描電子顯微鏡和隧道顯微鏡有什麼區別？

答：

掃描顯微鏡	隧道顯微鏡
它用於薄樣品	它具有較大的深度
透過樣品的透射電子形成物體的投影影像。	由樣品產生的二次電子形成影像。
類似於傳統的複合顯微鏡	類似於立體光學顯微鏡
易於使用	需要培訓
樣品製備簡單	樣品製備費力

Q5. 我們能否改變複合顯微鏡的放大倍數？如何？

答：複合顯微鏡的放大倍數由下式給出：

$$\mathrm{m=-\frac{L}{f_{0}}\frac{D}{f_{e}}}$$

其中 L = 顯微鏡筒長或目鏡與第二透鏡之間的距離

D = 最近清晰視覺距離

$\mathrm{f_{0}}$ = 物鏡的焦距

$\mathrm{f_{e}}$ = 目鏡的焦距

如果我們增加顯微鏡筒長，我們可以增加複合顯微鏡的放大倍數。因為放大倍數與顯微鏡筒長成正比。我們還可以看到，使用短焦距的透鏡也會增加顯微鏡的放大倍數。