簡併軌道

---

簡介

簡併軌道是指同一亞層中具有相同能級的電子軌道。如果磁場不干擾這些軌道，則簡併軌道始終存在。簡併性會干擾磁場的應用方式。

透過視覺化學習物質和化合物的知識是化學課程的關鍵組成部分。在這裡，我們將透過理解簡併軌道的含義以及 Aufbau 原理和 Hund 規則的相關概念，來學習原子的基本結構。

Hund 最大多重性規則

• 根據 Hund 最大多重性規則，對於特定的電子構型，具有最大多重性的項具有最低的能量。根據該規則，p、d 和 f 軌道中的電子只有在每個軌道中都存在一個電子或完全填充時才會配對。

• 電子填充簡併軌道。

• 根據弗里德里希·洪特的 Hund 多重性定律，在亞層中，每個軌道先填充一個電子，然後再向任何軌道填充第二個電子。

• 電子始終以相同的自旋量子數填充亞層，直到每個軌道中至少有一個電子。

• 在特定電子構型中，Hund 的多重性規則指出，在 f、p 和 d 軌道中，電子配對永遠不會發生，直到亞層中的每個軌道都填充了一個電子。假設一個碳原子具有電子構型 1𝑠22𝑠22𝑝2。根據 Hund 規則，2 個 2s 電子將填充該軌道，而 2 個 2p 電子將填充其他每個軌道。

什麼是 Hund 規則？

根據 Hund 的電子規則，簡併軌道會均勻地被佔據，然後再佔據較高能級的電子。Aufbau 原理、泡利不相容原理和 Hund 規則是解釋電子在後續能級中填充的三個概念。

Hund 規則的假設

• 根據該規則，在亞層中，一個軌道先被填充，然後再被另一個軌道佔據。

• 在各個軌道中的電子的自旋與跨多個軌道的電子的自旋相同。

Hund 規則的描述

當電子接近軌道時，它們彼此配對。這些帶負電的原子彼此排斥。由於它們不共享軌道，因此電子之間的排斥力較小。

當我們分析第二條規則時，單獨填充的軌道中未配對電子的自旋是相同的。該能級上第一個電子的自旋決定了亞層中所有其他電子的自旋。這在 𝐶 原子的電子構型（為 1𝑠22𝑠22𝑝2）中是一個例子。根據 Hund 規則，2 個 2s 電子將佔據相同的軌道，但 2 個 2p 電子將佔據不同的軌道。

什麼是 Aufbau 原理？

根據 Aufbau 原理，電子從較低能級開始，按照從低到高的順序填充能級。電子以遞增的 n+l 值填充，其中 n 是主量子數，l 是角量子數。這個概念有助於預測原子可能形成的化學鍵型別。

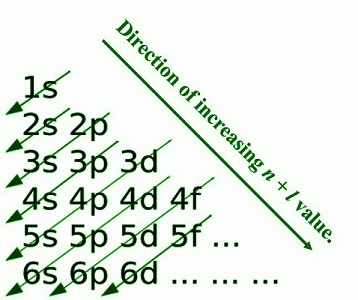
Goodphy，Madelung 規則圖，CC BY-SA 4.0

簡併軌道示例

這是一個簡併軌道的示例。

示例 - s、p、d 和 f 是構成原子的 4 個軌道。p 軌道中有 3 個軌道：𝑝𝑥、𝑝𝑦 和 𝑝𝑧。由於這 3 個軌道的能量相同並且對應於相同的軌道 (p)，因此它們被稱為簡併分子軌道。每個軌道先填充一個電子，然後是具有相反自旋的下一個電子填充相同的軌道。最終，p 軌道被佔據，3 個軌道各包含 6 個電子。

使用圖表解釋簡併軌道

為了視覺化這個概念，讓我們透過使用圖表對簡併軌道進行詳細的解釋。2p 軌道的電子填充過程需要 2𝑝𝑥、2𝑝𝑦 和 2𝑝𝑧。這些軌道彼此之間具有相同的能量。3p 軌道的電子填充過程也包括 3𝑝𝑥、3𝑝𝑦 和 3𝑝𝑧。簡併分子軌道是指具有相同能級的軌道。由於 4p 中的 4𝑝𝑥、4𝑝𝑦 和 4𝑝𝑧 電子彼此之間具有相同的能級，因此它們也是簡併的。現在讓我們使用圖形表示來評估這些能量亞層簡併性。

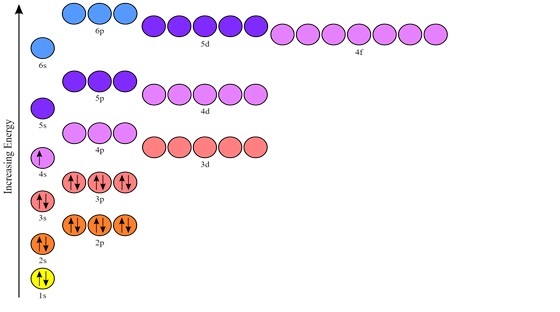
CK-12 基金會，鉀的軌道表示圖，CC BY-SA 3.0

結論

可以得出結論，簡併軌道是具有相同能級的電子軌道。任何外部影響（例如電場/磁場）都不會影響軌道的電子。這些軌道的簡併性會干擾磁場的應用。具有相同能量的是簡併軌道。軌道填充的原子是最穩定的原子，並且不會與其他元素相互作用。根據弗里德里希·洪特，在基態電子構型中，任何亞層中的大多數電子自旋都是平行的。Aufbau 原則預測電子將佔據從低到高的能級。p、d 和 f 軌道的簡併度值分別為 3、5 和 7。

常見問題

1. 當 3d 軌道被填充時，下一個電子將進入哪裡？

如 Aufbau 原理所述，電子將從較低能級躍遷到較高能級。電子將進入 4p 軌道，因為它比 3d 軌道具有更高的能級。

2. 什麼導致簡併？

泡利不相容原理禁止粒子在彼此非常靠近時具有相同的能量，這會導致粒子相互排斥。由此產生的簡併壓力與熱壓力相反，它僅取決於密度，而不取決於溫度。

3. Hund 規則在何種簡併軌道中失效？

每個具有相同能量的軌道必須先填充一個具有相同自旋的電子，然後才能在同一軌道中填充兩個電子，這與 Hund 規則相矛盾。這些電子的排列違反了 Hund 規則。

4. 3d 軌道完全佔據後，進入的電子將進入哪個軌道？

根據 Aufbau 原理，當電子到達時，它會從較低能級躍遷到較高能級。如果第三個軌道已滿，則電子將進入下一個較高能級軌道，即 4p 軌道。

5. 描述簡併特徵值？

如果多個線性無關的本徵態屬於給定的特徵值，則該特徵值被稱為簡併。經典和量子力學問題都可能發生簡併，它幾乎總是與系統的空間對稱性相關。