資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究樹中子樹DFS的C++查詢
在這個問題中，我們給定一棵二叉樹，我們需要從一個特定的節點執行dfs，在這個節點中，我們假設給定的節點作為根節點並從中執行dfs。
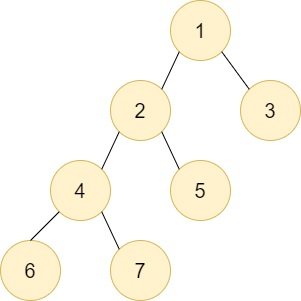
在上圖中，假設我們需要從節點F執行DFS
在本教程中，我們將應用一些非正統的方法，以便它可以大大降低我們的時間複雜度，因此我們也能夠為更高的約束執行此程式碼。
方法 - 在這種方法中，我們不會簡單地走樸素的方法，即我們只是對每個節點應用dfs，因為它不適用於更高的約束，因此我們嘗試使用一些非正統的方法來避免出現TLE。
#include <bits/stdc++.h>
using namespace std;
#define N 100000
// Adjacency list to store the
// tree nodes connections
vector<int> v[N];
unordered_map<int, int> mape; // will be used for associating the node with it's index
vector<int> a;
void dfs(int nodesunder[], int child, int parent){ // function for dfs and precalculation our nodesunder
a.push_back(child); // storing the dfs of our tree
// nodesunder of child subtree
nodesunder[child] = 1;
for (auto it : v[child]) { // performing normal dfs
if (it != parent) { // as we the child can climb up to
//it's parent so we are trying to avoid that as it will become a cycle
dfs(nodesunder, it, child); // recursive call
nodesunder[child] += nodesunder[it]; // storing incrementing the nodesunder
//by the number of nodes under it's children
}
}
}
// Function to print the DFS of subtree of node
void printDFS(int node, int nodesunder[]){
int ind = mape[node]; // index of our node in the dfs array
cout << "The DFS of subtree " << node << ": ";
// print the DFS of subtree
for (int i = ind; i < ind + nodesunder[node]; i++){ // going through dfs array and then
//printing all the nodes under our given node
cout << a[i] << " ";
}
cout << endl;
}
void addEdgetoGraph(int x, int y){ // for maintaining adjacency list
v[x].push_back(y);
v[y].push_back(x);
}
void mark(){ // marking each node with it's index in dfs array
int size = a.size();
// marks the index
for (int i = 0; i < size; i++) {
mape[a[i]] = i;
}
}
int main(){
int n = 7;
// add edges of a tree
addEdgetoGraph(1, 2);
addEdgetoGraph(1, 3);
addEdgetoGraph(2, 4);
addEdgetoGraph(2, 5);
addEdgetoGraph(4, 6);
addEdgetoGraph(4, 7);
// array to store the nodes present under of subtree
// of every node in a tree
int nodesunder[n + 1];
dfs(nodesunder, 1, 0); // generating our nodesunder array
mark(); // marking the indices in map
// Query 1
printDFS(2, nodesunder);
// Query 2
printDFS(4, nodesunder);
return 0;
}輸出
The DFS of subtree 2: 2 4 6 7 5 The DFS of subtree 4: 4 6 7
理解程式碼
在這種方法中，我們預先計算dfs的順序並將其儲存在一個向量中，現在當我們預先計算了dfs時，我們還計算從每個節點開始的每個子樹下存在的節點，然後我們簡單地從該節點的起始索引遍歷到其子樹內所有節點的數量。
結論
在本教程中，我們解決了一個問題，以解決樹中子樹的DFS查詢。我們還學習了此問題的C++程式以及解決此問題的完整方法（正常方法）。
我們可以用其他語言（如C、Java、Python和其他語言）編寫相同的程式。希望本文對您有所幫助。
更新於： 2021年11月25日
289 次瀏覽
廣告