資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究使用 C++ 統計曼哈頓距離相等的路徑數
給定變數 x1、x2、y1、y2，表示二維座標系上的兩個點 (x1, y1) 和 (x2, y2)。目標是找到所有路徑，這些路徑的距離等於這兩個點之間的曼哈頓距離。
曼哈頓距離
兩個點 (x1, y1) 和 (x2, y2) 之間的曼哈頓距離為 -
MD= |x1 – x2| + |y1 – y2|
令 A= |x1 – x2| 和 B= |y1 – y2|
所有曼哈頓距離等於 MD 的路徑的邊數都為 (A+B)。A 條水平邊和 B 條垂直邊。因此，(A+B) 條邊分成 2 組的可能組合為 ( A + B )CB = ( A+B )! / (A!)(B!)
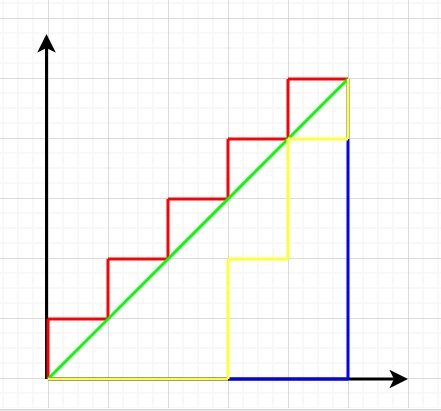
讓我們透過示例來理解
輸入
輸出 - 網格中給定方向的可能移動次數為 - 6
說明
Choosing move {1,1} = (1,1) → (2,2) → (3,3) - 3 steps
Choosing move {0,-1} = (3,2) → (3,3) → (3,2) → (3,1) - 3 steps
Total 6 steps.輸入 - A = 4, B = 4, x =2, y = 2; moves = {2, 1}, { -2, -3 }
輸出 - 網格中給定方向的可能移動次數為 - 2
說明
Choosing move {2,1} = (2,2) → (4,3) - 2 steps
Choosing move {-2,-3} = (2,0) X out of bound
Total 2 steps.下面程式中使用的演算法如下
在這種方法中，我們將建立一個向量來表示步驟，作為 pair<int,int>。從點 x,y 開始遍歷。從向量中選擇一個步驟，並選擇兩個方向（x 軸和 y 軸）中取值的最小值。選擇的最小值將允許進行更多移動。
為了沿特定方向移動，如果當前位置 x（或 y）> n（或 m），則到達 n（或 m）的移動次數為 ( n - 當前位置 )/x。如果小於，則到達 1 的移動次數為 ( 當前位置 - 1 )/x。
建立一個包含 0 和 1 的陣列 arr[]。
函式 count_cars(int arr[], int size) 以陣列和長度作為輸入，並返回透過汽車的數量。
將初始計數設定為 0。
從索引 i=0 遍歷陣列到 i<length-1。
如果 arr[i] 為 0，則再次從索引 j=i+1 遍歷陣列到 j<length。
對於每個 arr[j] 為 1，將計數增加 1，因為對 (arr[i],arr[j]) 為 (0,1) 且 i<j。
最後我們將得到總計數。
返回計數作為結果。
示例
#include <bits/stdc++.h>
using namespace std;
long long int bio_coeff(int A, int B){
long long int temp = 1;
if (B > A - B){
B = A - B;
}
for (int i = 0; i < B; ++i){
temp = temp * (A - i);
temp = temp / (i + 1);
}
return temp;
}
long long int Manhattan_distance(int x1, int y1, int x2, int y2){
int A = abs(x1 - x2);
int B = abs(y1 - y2);
int count = bio_coeff(A + B, B);
return count;
}
int main(){
int x1 = 6, y1 = 8, x2 = 2, y2 = 10;
cout<<"Count of paths with distance equal to Manhattan distance are: "<<
Manhattan_distance(x1, y1, x2, y2);
return 0;
}輸出
如果我們執行以上程式碼，它將生成以下輸出 -
Count of paths with distance equal to Manhattan distance are: 15
382 次瀏覽
