檢查是否可以透過在 Python 中旋轉向量 A 並新增向量 C 來到達向量 B

假設我們在二維平面上有三個向量 x、y 和 z。我們必須檢查是否可以透過將向量 x 旋轉 90 度（順時針）或根據需要多次新增向量 z 來從向量 x 獲取向量 y。

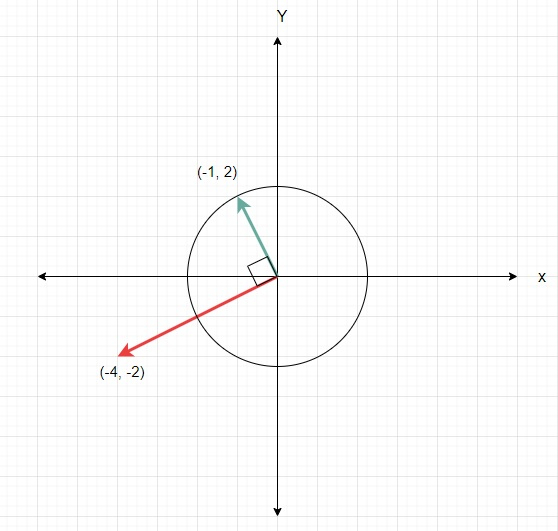
因此，如果輸入類似於 x = (-4, -2) y = (-1, 2) z = (-2, -1)，則輸出將為 True，因為我們可以將 z 與 x 相加得到位置 (-2, -1)，然後順時針旋轉 90° 得到 (-1, 2)。

要解決此問題，我們將遵循以下步驟：

定義一個函式 util()。這將接收 p、q、r、s

  • d := r * r + s * s
  • 如果 d 等於 0，則
    • 當 p 和 q 都為 0 時返回 true，否則返回 false
  • 當 (p * r + q * s) 和 (q * r - p * s) 都能被 d 整除時返回 true，否則返回 false
  • 從主方法執行以下操作：
  • 如果 util(x of p - x of q, y of p - y of q, x of r, y of r) 或 util(x of p + x of q, y of p + q[1], x of r, y of r) 或 util(x of p - y of q, y of p + x of q, x of r, y of r) 或 util(x of p + y of q, y of p - x of q, x of r, y of r) 中的任何一個為 true，則
    • 返回 True
  • 返回 False

示例

讓我們檢視以下實現以更好地理解：

 線上演示

def util(p, q, r, s):
   d = r * r + s * s
   if d == 0:
      return p == 0 and q == 0
   return (p * r + q * s) % d == 0 and (q * r - p * s) % d == 0
def solve(p,q,r):
   if util(p[0] - q[0], p[1] - q[1], r[0], r[1]) or util(p[0] + q[0], p[1] + q[1], r[0], r[1]) or util(p[0] - q[1], p[1] + q[0], r[0], r[1]) or util(p[0] + q[1], p[1] - q[0], r[0], r[1]):
      return True
   return False
p = (-4, -2)
q = (-1, 2)
r = (-2, -1)
print(solve(p, q, r))

輸入

(-4, -2), (-1, 2), (-2, -1)

輸出

True

更新於：2021年1月18日

53 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習
廣告