應用Python程式設計解決機械工程問題

---

使用Python程式設計解決PDV工作問題

在封閉系統（也稱為質量不變的系統）中，系統與其周圍環境透過熱量或功進行相互作用。在本文中，我們將處理非耗散功相互作用，也稱為PDV或位移功。我們將使用Python程式設計來解決這些問題。

但在我們開始之前，應該瞭解位移功的基本含義。位移功被評估為系統在以下壓力-體積圖中，在兩個端態之間所走路徑的積分。

要評估此功，必須完全指定路徑，這隻有在過程是準靜態的情況下才可能。在圖中，曲線（1-2）下的面積就是所做的功。數學上，它寫成如下：

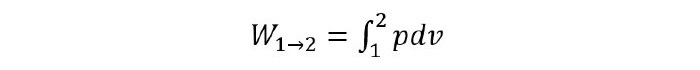
以下是典型過程1-2的壓力-體積圖：

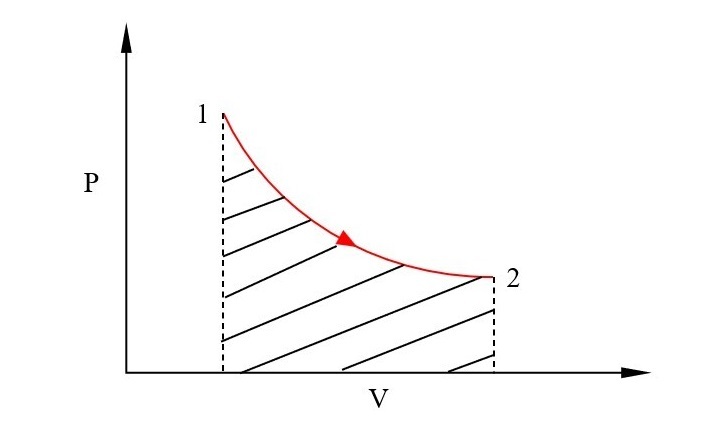
實現

現在，正如我們已經提到的，要評估PDV功，必須完全指定路徑。因此，要在Python中實現它，需要知道壓力和體積之間的關係。此外，還應預先知道關於壓力或體積的端點資訊。解決問題的步驟如下：

• 必須開發一個函式來指定p和v之間的關係。
• 需要提供輸入引數。
• 必須根據輸入資料計算右側的常數。
• 需要提供端點之間要建立的資料點數（n）。
• 計算資料點之間的間距（h）並建立體積陣列。
• 將使用數值積分來解決問題。
• 最後，要繪製過程，將使用Pylab（一個用於繪圖的python模組）以及NumPy。

數學公式

對於端點a和b之間的函式f(x)，可以使用梯形法則簡單地執行數值積分，如下所示：

這裡，索引i從0開始到n結束。所以，x₀=a，x_n=b。

過程pv=常數

為了理解這個過程，讓我們首先考慮一個壓力-體積關係由pv=c給出的問題。我們將分段編寫程式碼並在每個部分之後解釋它在做什麼。

# importing modules
from pylab import *
from numpy import *

在本部分程式碼中，分別呼叫了‘pylab’和‘numpy’模組用於資料繪圖和陣列建立。

# defining function for pv relation
def p(v,C):
    return C/v

這裡，定義了一個函式，它接受兩個引數，即體積和常數C（pv=c的右側）。可以根據給定的熱力學過程和初始條件修改此函式。

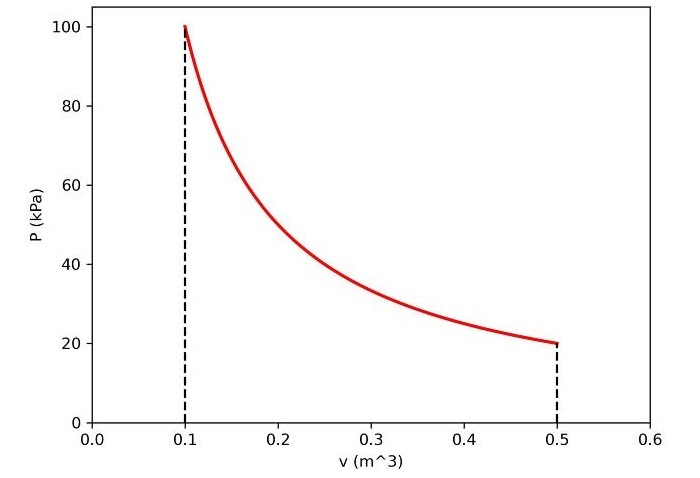
# input data
#---------------
# Initial and final volume (in m^3)
v1 = 0.1 
v2 = 0.5
# initial pressure (in kPa)
p1 = 100

然後將輸入資料提供給程式。在本問題中，我們假設端點的體積以及初始壓力是已知的。

# Evaluating C
C=p1*v1

# Number of data points between end points
n=5000

# Spacing between data points
h=(v2-v1)/n

# creating array of volume
v=linspace(v1, v2,n)

根據輸入資料計算常數C。需要提供端點之間的資料點數（因為我們使用了梯形法則，所以資料點數越多，精度越高）。計算資料點之間的間距並建立體積陣列。

# Numerical Integration
f_a=p(v1,C)
f_b=p(v2,C)
Sum=0
for i in range(1,n-1):
    Sum=Sum+p(v[i],C)
I=h*((f_a+f_b)/2+Sum)

# work done
Work = I

print(f'Work = {round(Work,3)} kJ')

在此步驟中，使用上一節中提到的公式執行數值積分。然後將積分結果傳遞給變數‘Work’（為簡單起見）並列印結果。為了繪製過程，可以使用以下程式碼段，該程式碼段使用 print()函式執行繪圖任務。

# Data plotting
figure(1,dpi=300)
plot(v,p(v,C),'r',linewidth=2)
xlabel('v (m^3)')
ylabel('P (kPa)')

ylim(0,p1+5)
xlim(0,v2+0.1)
plot([v1,v1],[0,p1],'--k')

p2=C/v2
plot([v2,v2],[0,p2],'--k')
savefig('work.jpg')

程式輸出如下：

Work = 16.091 kJ

過程pv^n=c

假設我們已經計算了pv^n過程中所做的功，其中n對我們已知。這次我們將假設端點的壓力以及初始體積是已知的。這次唯一變化的是我們將為p-v關係和輸入引數建立的函式。

這裡我們假設v1、v2和p1分別為0.1 m3、0.3 m3和200 kPa。另外，假設n=1.4。計算該過程中所做的功以及資料繪圖的Python程式如下：

# importing modules
from pylab import *
from numpy import *

# defining function for pv relation
def p(v,C,N):
    return C/v**N

# input data
#---------------
# Initial and final volume (in m^3)
v1 = 0.1 
v2 = 0.3
# initial pressure (in kPa)
p1 = 200 
# Exponent n
N=1.4

# Evaluating C
C=p1*v1**N


# Number of data points between end points
n=5000

# Spacing between data points
h=(v2-v1)/n

# creating array of volume
v=linspace(v1, v2,n)

# Numerical Integration
f_a=p(v1,C,N)
f_b=p(v2,C,N)
Sum=0
for i in range(1,n-1):
    Sum=Sum+p(v[i],C,N)
I=h*((f_a+f_b)/2+Sum)

# work done
Work2 = I

print(f'Work = {round(Work2,3)} kJ')

# Data plotting
figure(1,dpi=300)
plot(v,p(v,C,N),'r',linewidth=2)
xlabel('v (m^3)')
ylabel('P (kPa)')

ylim(0,p1+5)
xlim(0,v2+0.1)
plot([v1,v1],[0,p1],'--k')

p2=C/v2**N
plot([v2,v2],[0,p2],'--k')
savefig('work2.jpg')

程式輸出如下：

Work = 17.777 kJ

在本文中，您已經觀察到如何藉助Python評估封閉系統的功。上述程式可以輕鬆地應用於不同的過程或不同的初始條件，只需稍微更改函式、陣列和輸入引數即可。