環形

---

簡介

環形（複數為 annuli 或 annuluses）兩個同心圓之間的區域。名稱“環形”源自拉丁詞 annulus 或 annulus，意思是“小環”。Annular 是形容詞形式（如環形日食）。開放環形和穿孔平面在拓撲上彼此相等。環形是兩個同心圓或具有兩個以上旋轉中心的圓之間的內部空間。本文將向您介紹環形的多種數學用途，它具有環狀形狀。日常生活中的例子包括指環、甜甜圈等。為了更好地理解這個概念，讓我們進一步研究環形的形狀，並透過一些例子進行練習。

環形：圓形環（定義）

• 環形是一種二維平面圖形，具有圓形形狀，由兩個同心圓組成。

• 環形是這兩個同心環之間形成的區域或面積。由於它是一個具有圓形的平面圖形，因此邊緣是兩個具有相同中心的圓。

• 由於物體的中心有一個圓，因此它看起來像一個圓盤。

• 單詞“環形”源自拉丁語“annuli”，意思是“小環”。

• 環形類似於投擲環或圓盤，因為它扁平且圓形，中間有一個孔。

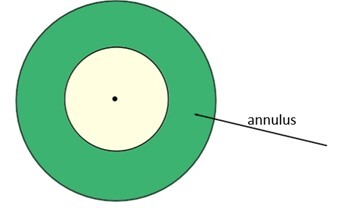
• 請檢視下面的插圖，其中有兩個圓——一個小圓，也稱為內圓，一個大圓，通常稱為外圓。這兩個圓的中心都位於黑色標記的位置。環形是這兩個圓邊緣之間呈綠色的區域。

周長和麵積

• 二維形狀的周

• 長是圍繞它的空間。環形也可以稱為環，因為它是由兩個同心圓組成的扁平圓形。因此，穿孔平面和圓柱體可以被認為是開放環的拓撲等價物。與面積類似，為了獲得環形的周長，我們必須考慮內圓和外圓。然後，透過將大和小的圓的半徑相加並乘以 2 來確定環或環形的周長。使用以下公式計算周長：

  $$\mathrm{環形周長=2π(R+r)}$$

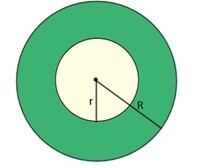
  其中 R 是外環的半徑，r 是小環的半徑。

• 環形區域是指環形空間的面積，或兩個同心圓之間的封閉區域。為了確定環形的面積，我們必須知道內圓和外圓的面積。環形的尺寸由兩個半徑 R 和 r 定義，分別對應於外環和內環的半徑。當我們知道這兩個半徑的尺寸時，我們可以透過從大圓的面積中減去小圓的面積來計算面積。因此，使用以下公式確定環形的面積：

  $$\mathrm{環形面積=π(R^2-r^2)}$$

  其中 R 是外環的半徑，r 是小環的半徑。

解題示例

1)如果環形的外半徑為 12 個單位，內半徑為 6 個單位，則計算其面積。

答案

已知

$$\mathrm{R=12\: \&\: r=6}$$

因此，使用環形面積公式，我們得到；

$$\mathrm{環形面積=π(R^2-r^2 )}$$

$$\mathrm{=π(12^2-6^2 )}$$

$$\mathrm{=π(144-36)=108π\: 平方單位}$$

2)如果外半徑為 14 個單位，內半徑為 9 個單位，則計算環形的周長。

答案

已知

$$\mathrm{R=14\: \&\: r=9}$$

因此，使用環形周長公式，我們得到；

$$\mathrm{環形周長=2π(R+r)=2π(14+9)=2π(23)=46π\: 單位}$$

3)鋼管橫截面的面積是多少，其外半徑為 100 個單位，內半徑為 50 個單位？

答案

已知

$$\mathrm{R=100\: \&\: r=50}$$

因此，使用環形面積公式，我們得到；

$$\mathrm{環形面積=π(R^2-r^2)=π(100^2-50^2)=π(150)(50)=7500π\: 平方單位}$$

因此，鋼管橫截面的面積為 7500π 平方單位

4)求周長為 18π 且外半徑為 7 釐米的環形的內半徑。

答案

已知

$$\mathrm{R=7\: \&\: r=?}$$

因此，使用環形周長公式，我們得到；

$$\mathrm{環形周長=2π(R+r)=2π(7+r)}$$

$$\mathrm{18π=2π(7+r)}$$

$$\mathrm{\frac{18}{2}=r+7}$$

$$\mathrm{r=9-7=2}$$

因此，內圓的半徑為 2 釐米。

5)DVD 光碟的面積是多少，其外半徑為 100 個單位，內半徑為 50 個單位？

答案

已知

$$\mathrm{R=100\: \&\: r=50}$$

因此，使用環形面積公式，我們得到；

環形面積=π(R²-r²)=π(100²-50²)=π(150)(50)=7500π 平方單位。因此，DVD 光碟的面積為 7500π

6)如果環形的外半徑為 14 個單位，內半徑為 7 個單位，則計算其面積。

答案

已知

$$\mathrm{R=14\: \&\: r=7}$$

因此，使用環形面積公式，我們得到；

環形面積=π(R²-r²)=π(14²-7²)=π(196-49)=147π 平方單位

7)求周長為 20π 且外半徑為 8 釐米的環形的內半徑。

答案

已知

$$\mathrm{R=8\: \&\: r=?}$$

因此，使用環形周長公式，我們得到；

$$\mathrm{環形周長=2π(R+r)=2π(8+r)}$$

$$\mathrm{20π=2π(8+r)}$$

$$\mathrm{\frac{20}{2}=r+8}$$

$$\mathrm{r=10-8=2}$$

因此，內圓的半徑為 2 釐米。

結論

• 環形是一種二維平面圖形，具有圓形形狀，由兩個同心圓組成。環形是這兩個同心圓之間形成的區域或面積。

• 環形面積=π(R²-r²)，其中 R 是外環的半徑，r 是小環的半徑。

• 環形周長=2π(R+r)，其中 R 是外環的半徑，r 是小環的半徑。

常見問題

1. 環形有幾條邊？

環形是一種類似於環的平面形狀。它有兩個具有相同中心的圓作為其邊緣。環形物體是指具有環形形狀的物體。

2. 環形的定義是什麼？

環形是由兩個圓連線而成的形狀。環形是由兩個同心圓（共享一個共同中心的圓）的交點形成的平面圖形。環形具有環的形狀。

3. 環形是圓的哪一部分？

環形是兩個圓的外邊緣之間的空間。兩個圓的外邊緣之間的區域始終類似於中間有一個孔的圓。兩個同心圓的差形成一個環形。

4. 環形可以是正方形嗎？

根據切片方式，環形可以解釋為閉合弦單點函式的平方或開放弦雙點函式。

5. 什麼是環形表面？

環形表面是由圓組成的單一曲率線系統組成的表面。考慮接觸兩個連續表面球體的球體：這些球體形成一個特殊的線性同餘；它們必須接觸球體。