資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究給定起始字元的最長連續路徑
提供一個由不同字元組成的矩陣。從一個字元開始，我們必須找到透過所有比當前字元大的字元的最長路徑。這些字元是相互連的。
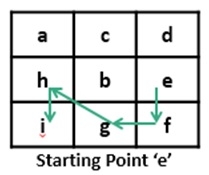
要找到最長路徑，我們將使用深度優先搜尋演算法。在進行深度優先搜尋時，可能會多次出現一些子問題。為了避免重複計算，我們將使用動態規劃方法。
輸入和輸出
Input: The matrix as shown above. And the starting point. Here the starting point is e. Output: Enter Starting Point (a-i): e Maximum consecutive path: 5
演算法
findLongestLen(i, j, prev)
輸入： 位置 i 和 j 以及前一個字元。
輸出：最長長度。
Begin if (i, j) place is valid or prev and matrix[i,j] are adjacent, then return 0 if longestPath[i, j] is already filled, then return longestPath[i, j] len := 0 for all its nearest 8 rooms k, do len := maximum of len and (1 + findLongestLen(i, x[k], j +y[k], matrix[i, j])) done longestPath[i, j] := len return len End
getLen(start)
輸入 - 起始點。
輸出 - 最大長度。
Begin for all row r of matrix, do for all column c, of matrix, do if matrix[i, j] = start, then for all adjacent room k, do len := maximum of len and (1 + findLongestLen(i, x[k], j +y[k], matrix[i, j]))) done done done return len End
示例
#include<iostream>
#define ROW 3
#define COL 3
using namespace std;
// tool matrices to recur for adjacent cells.
int x[] = {0, 1, 1, -1, 1, 0, -1, -1};
int y[] = {1, 0, 1, 1, -1, -1, 0, -1};
int longestPath[ROW][COL];
char mat[ROW][COL] = {
{'a','c','d'},
{'h','b','a'},
{'i','g','f'}
};
int max(int a, int b) {
return (a>b)?a:b;
}
bool isvalid(int i, int j) {
if (i < 0 || j < 0 || i >= ROW || j >= COL) //when i and j are in range
return false;
return true;
}
bool isadjacent(char previous, char current) {
return ((current - previous) == 1); //check current and previous are adjacent or not
}
int findLongestLen(int i, int j, char prev) {
if (!isvalid(i, j) || !isadjacent(prev, mat[i][j])) //when already included or not adjacent
return 0;
if (longestPath[i][j] != -1)
return longestPath[i][j]; //subproblems are solved already
int len = 0; // Initialize result to 0
for (int k=0; k<8; k++) //find length of the largest path recursively
len = max(len, 1 + findLongestLen(i + x[k], j + y[k], mat[i][j]));
return longestPath[i][j] = len; // save the length and return
}
int getLen(char start) {
for(int i = 0; i<ROW; i++)
for(int j = 0; j<COL; j++)
longestPath[i][j] = -1; //set all elements to -1
int len = 0;
for (int i=0; i<ROW; i++) {
for (int j=0; j<COL; j++) { // check for all possible starting point
if (mat[i][j] == start) {
for (int k=0; k<8; k++) //for all eight adjacent cells
len = max(len, 1 + findLongestLen(i + x[k], j + y[k], start));
}
}
}
return len;
}
int main() {
char start;
cout << "Enter Starting Point (a-i): "; cin >> start;
cout << "Maximum consecutive path: " << getLen(start);
return 0;
}輸出
Enter Starting Point (a-i): e Maximum consecutive path: 5
更新時間： 16-6-2020
324 次瀏覽
廣告