Javascript 中的 AVL 樹旋轉

為了保持平衡，AVL 樹可能會執行以下四種旋轉：

• 左旋轉
• 右旋轉
• 左-右旋轉
• 右-左旋轉

前兩種旋轉是單旋轉，後兩種旋轉是雙旋轉。要使樹不平衡，我們至少需要高度為 2 的樹。透過這棵簡單的樹，讓我們逐一瞭解它們。

左旋轉

如果在右子樹的右子樹中插入節點時樹變得不平衡，則我們執行單左旋轉：

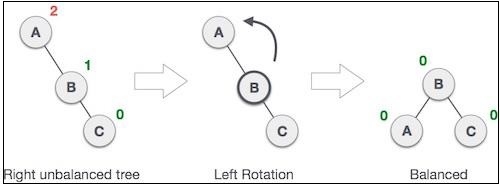
在我們的示例中，節點 **A** 由於在 A 的右子樹中插入了一個節點而變得不平衡。我們透過使 **A** 成為 **B** 的左子樹來執行左旋轉。這種旋轉也稱為 LL 旋轉。讓我們看看如何實現它：

function rotationLL(node) {
let tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}

右旋轉

如果在左子樹的左子樹中插入節點，AVL 樹可能會變得不平衡。然後樹需要右旋轉。

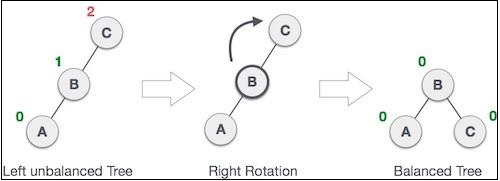
如圖所示，透過執行右旋轉，不平衡的節點成為其左子節點的右子節點。這也被稱為 RR 旋轉。讓我們看看程式碼中它是如何實現的：

function rotationRR(node) {
let tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}

左-右旋轉

雙旋轉是已經解釋過的旋轉版本的稍微複雜一些的版本。為了更好地理解它們，我們應該注意旋轉過程中執行的每個動作。讓我們首先檢查如何執行左-右旋轉。左-右旋轉是左旋轉後跟著右旋轉的組合。

狀態	動作
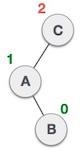	已將節點插入左子樹的右子樹中。這使得 **C** 成為不平衡節點。這些情況會導致 AVL 樹執行左-右旋轉。
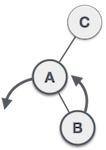	我們首先對 **C** 的左子樹執行左旋轉。這使得 **A** 成為 **B** 的左子樹。
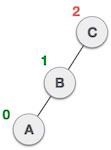	節點 **C** 仍然不平衡，但是現在，這是因為左子樹的左子樹。
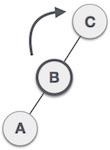	我們現在將對樹進行右旋轉，使 **B** 成為這個子樹的新根節點。**C** 現在成為其自身左子樹的右子樹。
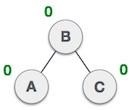	樹現在已平衡。

這也被稱為 LR 旋轉，因為我們首先執行左旋轉，然後執行右旋轉。可以使用之前的兩種方法按如下方式實現：

function rotationLR(node) {
node.left = rotationRR(node.left);
return rotationLL(node);
}

右-左旋轉

第二種型別的雙旋轉是右-左旋轉。它是右旋轉後跟著左旋轉的組合。

狀態	動作
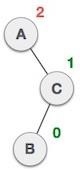	已將節點插入右子樹的左子樹中。這使得 **A** 成為一個不平衡節點，平衡因子為 2。
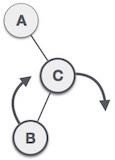	首先，我們在 **C** 節點沿進行右旋轉，使 **C** 成為其自身左子樹 **B** 的右子樹。現在，**B** 成為 **A** 的右子樹。
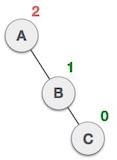	節點 **A** 仍然不平衡，因為其右子樹的右子樹需要左旋轉。
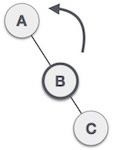	透過使 **B** 成為子樹的新根節點來執行左旋轉。**A** 成為其右子樹 **B** 的左子樹。
	樹現在已平衡。

這也被稱為 RL 旋轉，因為我們首先執行右旋轉，然後執行左旋轉。可以使用之前的兩種方法按如下方式實現：

function rotationRL(node) {
node.right = rotationLL(node.right);
return rotationRR(node);
}

Sai Subramanyam

更新於：2020年6月15日

274 次瀏覽

啟動你的 職業生涯

完成課程獲得認證

開始學習